limite și infinitezimale
calculul este de obicei dezvoltat prin lucrul cu cantități foarte mici. Din punct de vedere istoric, prima metodă de a face acest lucru a fost prin infinitesimale. Acestea sunt obiecte care pot fi tratate ca numere reale, dar care sunt, într-un anumit sens, „infinit de mici”. De exemplu, un număr infinitezimal ar putea fi mai mare decât 0, dar mai puțin decât orice număr din secvența 1, 1/2, 1/3, … și astfel mai puțin decât orice număr real pozitiv. Din acest punct de vedere, calculul este o colecție de tehnici de manipulare a infinitesimalelor. Simbolurile d x {\displaystyle dx}

și d y {\displaystyle dy}

au fost considerate infinitezimale, iar derivata d y / d x {\displaystyle dy/dx}

a fost pur și simplu raportul lor. abordarea infinitezimală a căzut în dizgrație în secolul al 19-lea, deoarece era dificil să se precizeze noțiunea de infinitezimal. Cu toate acestea, conceptul a fost reînviat în secolul 20 prin introducerea analizei non-standard și a analizei infinitesimale netede, care a oferit baze solide pentru manipularea infinitesimalelor.
la sfârșitul secolului al 19-lea, infinitesimalele au fost înlocuite în mediul academic de abordarea Epsilon, delta a limitelor. Limitele descriu valoarea unei funcții la o anumită intrare în ceea ce privește valorile sale la intrările din apropiere. Acestea surprind comportamentul la scară mică în contextul sistemului de numere reale. În acest tratament, calculul este o colecție de tehnici pentru manipularea anumitor limite. Infinitesimalele sunt înlocuite cu numere foarte mici, iar comportamentul infinit de mic al funcției se găsește luând comportamentul limitativ pentru numere din ce în ce mai mici. S-a crezut că limitele oferă o bază mai riguroasă pentru calcul și, din acest motiv, au devenit abordarea standard în secolul al XX-lea.
Calcul diferențial

calculul diferențial este studiul definiției, proprietăților și aplicațiilor derivatei unei funcții. Procesul de găsire a derivatului se numește diferențiere. Având în vedere o funcție și un punct din domeniu, derivata din acel punct este o modalitate de codificare a comportamentului la scară mică al funcției în apropierea acelui punct. Găsind derivata unei funcții în fiecare punct al domeniului său, este posibil să se producă o nouă funcție, numită funcție derivată sau doar derivata funcției originale. În termeni formali, derivata este un operator liniar care ia o funcție ca intrare și produce o a doua funcție ca ieșire. Acest lucru este mai abstract decât multe dintre procesele studiate în algebra elementară, unde funcțiile introduc de obicei un număr și produc un alt număr. De exemplu, dacă funcției de dublare i se dă intrarea trei, atunci iese șase, iar dacă funcției de pătrat i se dă intrarea trei, atunci iese nouă. Cu toate acestea, derivatul poate lua funcția de pătrat ca intrare. Aceasta înseamnă că derivata ia toate informațiile funcției de pătrat—cum ar fi faptul că două sunt trimise la patru, trei sunt trimise la nouă, patru sunt trimise la șaisprezece și așa mai departe-și folosește aceste informații pentru a produce o altă funcție. Funcția produsă prin derivarea funcției de pătrat se dovedește a fi funcția de dublare.
în termeni mai expliciți, „funcția de dublare” poate fi notată cu g(x) = 2x și „funcția de pătrat” cu f(x) = x2. „Derivatul” ia acum funcția f(x), definită de expresia „x2”, ca intrare, adică toate informațiile—cum ar fi că două sunt trimise la patru, trei sunt trimise la nouă, patru sunt trimise la șaisprezece și așa mai departe—și folosește aceste informații pentru a emite o altă funcție, funcția g (x) = 2x, așa cum se va dovedi.
cel mai comun simbol pentru o derivată este un semn apostrof numit prim. Astfel, derivata unei funcții numite f este notată cu f’, pronunțată”F prime”. De exemplu, dacă f(x) = x2 este funcția de pătrat, atunci f'(x) = 2x este derivata sa (funcția de dublare g de sus). Această notație este cunoscută sub numele de notația lui Lagrange.
Dacă intrarea funcției reprezintă timpul, atunci derivata reprezintă schimbarea în raport cu timpul. De exemplu, dacă f este o funcție care ia un timp ca intrare și dă poziția unei mingi la acel moment ca ieșire, atunci derivata lui f este modul în care poziția se schimbă în timp, adică este viteza mingii.
dacă o funcție este liniară (adică dacă graficul funcției este o linie dreaptă), atunci funcția poate fi scrisă ca y = mx + b, unde x este variabila independentă, y este variabila dependentă, b este y-intercepta și:
m = rise run = schimbare în y schimbare în X = hectolitru y X . {\displaystyle m={\frac {\text {rise}} {\text {run}}}={\frac {{\text {Modificare în }}y} {{\text {Modificare în }}x}}={\frac{\Delta y} {\Delta x}}.}

aceasta oferă o valoare exactă pentru panta unei linii drepte. Dacă graficul funcției nu este o linie dreaptă, atunci schimbarea în y împărțită la schimbarea în x variază. Derivatele dau o semnificație exactă noțiunii de schimbare a producției în ceea ce privește schimbarea intrărilor. Pentru a fi concret, lăsați f să fie o funcție și fixați un punct a în domeniul f. (a, f(A)) este un punct pe graficul funcției. Dacă h este un număr apropiat de zero, atunci a + h este un număr apropiat de a. prin urmare, (a + h, f(A + h)) este aproape de (a, f(a)). Panta dintre aceste două puncte este
m = f ( A + h ) − f ( A ) ( A + h ) − A = f ( A + h ) − f ( A ) h . {\displaystyle m={\frac {f(A+h)-f(a)} {(A+h)-a}}={\frac{f(A+h)-f(A)} {h}}.}

această expresie se numește coeficient de diferență. O linie prin două puncte pe o curbă se numește linie secantă, deci m este panta liniei secante dintre (A, f(A)) și (a + h, f(A + h)). Linia secantă este doar o aproximare a comportamentului funcției în punctul a, deoarece nu ține cont de ceea ce se întâmplă între a și a + h. nu este posibil să descoperiți comportamentul la a setând h la zero, deoarece acest lucru ar necesita împărțirea la zero, ceea ce este nedefinit. Derivata este definită luând limita ca H tinde la zero, ceea ce înseamnă că consideră comportamentul lui f pentru toate valorile mici ale lui h și extrage o valoare consistentă pentru cazul în care h este egal cu zero:
lim h 0 F ( A + h ) − f ( A ) h . {\displaystyle \ lim _{h \ la 0}{f (A+h) – f(a) \peste {h}}.}

Geometric, derivata este panta liniei tangente la graficul lui f la a. linia tangentă este o limită a liniilor secante la fel cum derivata este o limită a coeficienților de diferență. Din acest motiv, derivata este uneori numită panta funcției f.
Iată un exemplu particular, derivata funcției de pătrat la intrarea 3. Fie F ( x) = x2 funcția de pătrat.

f ′ ( 3 ) = lim h → 0 ( 3 + h ) 2 − 3 2 h = lim h → 0 9 + 6 h + h 2 − 9 h = lim h → 0 6 h + h 2 h = lim h → 0 ( 6 + h ) = 6 {\displaystyle {\begin{aligned}f'(3)&=\lim _{h\to 0}{(3+h)^{2}-3^{2} \over {h}}\\&=\lim _{h\to 0}{9+6h+h^{2}-9 \over {h}}\\&=\lim _{h\to 0}{6h+h^{2} \over {h}}\\&=\lim _{h\to 0}(6+h)\\&=6\end{aligned}}}

panta liniei tangente la funcția de pătrat în punctul (3, 9) este 6, adică merge de șase ori mai repede decât merge spre dreapta. Procesul limită descris poate fi efectuat pentru orice punct din domeniul funcției de pătrat. Aceasta definește funcția derivată a funcției de pătrat sau doar derivata funcției de pătrat pe scurt. Un calcul similar cu cel de mai sus arată că derivata funcției de pătrat este funcția de dublare.
notația Leibniz
o notație comună, introdusă de Leibniz, pentru derivata din exemplul de mai sus este
y = x 2 d y D x = 2 x . {\displaystyle {\begin{aligned}y&=x^{2}\\{\frac {dy}{dx}}&=2x.\end{aligned}}}

într-o abordare bazată pe limite, simbolul dy / dx trebuie interpretat nu ca coeficientul a două numere, ci ca o prescurtare a limitei calculate mai sus. Cu toate acestea, Leibniz a intenționat să reprezinte coeficientul a două numere infinitezimal mici, dy fiind schimbarea infinitezimal mică în y cauzată de o schimbare infinitezimal mică DX aplicată la x. de asemenea, ne putem gândi la d/dx ca la un operator de diferențiere, care ia o funcție ca intrare și dă o altă funcție, derivata, ca ieșire. De exemplu:
d d x ( x 2 ) = 2 x . {\displaystyle {\frac {d}{dx}}(x ^ {2})=2x.}

în această utilizare, dx în numitor este citit ca „cu privire la x”. Un alt exemplu de notație corectă ar putea fi:
g ( t ) = t 2 + 2 t + 4 d d t g ( t ) = 2 t + 2 {\displaystyle {\begin{aliniat}G(t)=T^{2}+2t+4\\\\{D \over DT}g(t)=2t+2\end{aliniat}}}

chiar și atunci când calculul este dezvoltat folosind limite mai degrabă decât infinitezimale, este obișnuit să manipulezi simboluri precum DX și Dy ca și cum ar fi numere reale; deși este posibil să se evite astfel de manipulări, ele sunt uneori convenabile din punct de vedere notațional în exprimarea operațiilor precum derivata totală.
calcul Integral
calculul Integral este studiul definițiilor, proprietăților și aplicațiilor a două concepte conexe, integrala nedeterminată și integrala definită. Procesul de găsire a valorii unei integrale se numește integrare. În limbajul tehnic, calculul integral studiază doi operatori liniari înrudiți.
integrala nedefinită, cunoscută și sub numele de antiderivativă, este operația inversă a derivatei. F este o integrală nedeterminată a lui f când f este o derivată a lui F. (Această utilizare a literelor mici și majuscule pentru o funcție și integrala sa nedeterminată este comună în calcul.)
integrala definită introduce o funcție și emite un număr, care dă suma algebrică a zonelor dintre graficul intrării și axa X. Definiția tehnică a integralei definite implică limita unei sume de zone de dreptunghiuri, numită sumă Riemann.un exemplu motivant sunt distanțele parcurse într-un anumit timp.
D I S t A N C E = S P e e d t I m e {\displaystyle \mathrm {Distance} =\mathrm {Speed} \cdot \mathrm {Time}}

dacă viteza este constantă, este necesară doar înmulțirea, dar dacă viteza se schimbă, este necesară o metodă mai puternică de a găsi distanța. O astfel de metodă este de a aproxima distanța parcursă prin împărțirea timpului în mai multe intervale scurte de timp, apoi înmulțirea timpului scurs în fiecare interval cu una dintre vitezele din acel interval și apoi luarea sumei (o sumă Riemann) a distanței aproximative parcurse în fiecare interval. Ideea de bază este că, dacă trece doar un timp scurt, atunci viteza va rămâne mai mult sau mai puțin aceeași. Cu toate acestea, o sumă Riemann oferă doar o aproximare a distanței parcurse. Trebuie să luăm limita tuturor acestor sume Riemann pentru a găsi distanța exactă parcursă.
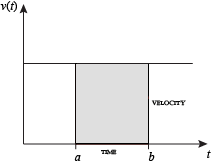

când viteza este constantă, distanța totală parcursă pe intervalul de timp dat poate fi calculată prin înmulțirea vitezei și timpului. De exemplu, o călătorie constantă de 50 mph timp de 3 ore are ca rezultat o distanță totală de 150 de mile. În diagrama din stânga, când viteza constantă și timpul sunt grafice, aceste două valori formează un dreptunghi cu înălțimea egală cu viteza și lățimea egală cu timpul scurs. Prin urmare, produsul vitezei și timpului calculează și aria dreptunghiulară sub curba vitezei (constantă). Această legătură între zona de sub o curbă și distanța parcursă poate fi extinsă la orice regiune de formă neregulată care prezintă o viteză fluctuantă pe o anumită perioadă de timp. Dacă f (x) în diagrama din dreapta reprezintă viteza, deoarece variază în timp, distanța parcursă (între timpii reprezentați de a și b) este aria regiunii umbrite s.
pentru a aproxima acea zonă, o metodă intuitivă ar fi împărțirea distanței dintre a și b într-un număr de segmente egale, lungimea fiecărui segment reprezentat de simbolul XQX. Pentru fiecare segment mic, putem alege o valoare a funcției f(x). Apelați această valoare h. apoi aria dreptunghiului cu baza Xixx și înălțimea h dă distanța (timpul Xixx înmulțită cu viteza h) parcursă în acel segment. Asociat cu fiecare segment este valoarea medie a funcției de deasupra acestuia, f(x) = h. suma tuturor acestor dreptunghiuri oferă o aproximare a zonei dintre axă și curbă, care este o aproximare a distanței totale parcurse. O valoare mai mică pentru Xixt va da mai multe dreptunghiuri și în majoritatea cazurilor o aproximare mai bună, dar pentru un răspuns exact trebuie să luăm o limită pe măsură ce Xixtx se apropie de zero.
simbolul integrării este un s alungit (S înseamnă”sum”). Integrala definită este scrisă ca: a b f ( x ) d x . {\displaystyle \ int _ {a}^{b}f(x)\,dx.}

și se citește „integrala de la A la b a lui f-of-x în raport cu x.” notația Leibniz dx este destinată să sugereze împărțirea ariei de sub curbă într-un număr infinit de dreptunghiuri, astfel încât lățimea lor să devină DX infinit de mic. Într-o formulare a calculului bazată pe limite, notația
A B A B A x {\displaystyle \int _{A}^{B}\cdots \,dx}

trebuie înțeleasă ca un operator care ia o funcție ca intrare și dă un număr, zona, ca ieșire. Diferențialul de terminare, dx, nu este un număr și nu este înmulțit cu f(x), deși, servind ca o reamintire a definiției limitei XIX, poate fi tratat ca atare în manipulările simbolice ale integralei. Formal, diferențialul indică variabila peste care este integrată funcția și servește ca suport de închidere pentru operatorul de integrare.
integrala nedefinită, sau antiderivativă, este scrisă:
f ( x ) d x . {\displaystyle \ int f (x)\, dx.}

funcțiile care diferă doar de o constantă au aceeași derivată și se poate arăta că antiderivativul unei funcții date este de fapt o familie de funcții care diferă doar de o constantă. Deoarece derivata funcției y = x2 + C, unde C este orice constantă, este y’ = 2x, antiderivativul acesteia din urmă este dat de:
2 x d x = x 2 + c . {\displaystyle \ int 2x\, dx = x^{2} + C.}

Constanta nespecificată C prezentă în integrala nedefinită sau antiderivativă este cunoscută sub numele de Constanta integrării.
Teorema fundamentală
Teorema fundamentală a calculului afirmă că diferențierea și integrarea sunt operații inverse. Mai exact, se referă valorile antiderivative la integrale definite. Deoarece este de obicei mai ușor să calculezi un antiderivativ decât să aplici definiția unei integrale definite, Teorema fundamentală a calculului oferă un mod practic de calcul al integralelor definite. De asemenea, poate fi interpretat ca o afirmație precisă a faptului că diferențierea este inversul integrării.
Teorema fundamentală a stărilor de calcul: Dacă o funcție f este continuă pe interval și dacă F este o funcție a cărei derivată este f pe interval (a, b), atunci
XV a b f ( x ) d x = F ( b ) − F ( a ) . {\displaystyle \ int _ {a}^{b}f (x)\, dx=F(b)-F(a).}

Mai mult, pentru fiecare x din intervalul (a, b),
d d x x f ( t ) d t = f ( x ) . {\displaystyle {\frac{d} {dx}}\int _{a}^{x}f(t)\, dt=f(x).}

această realizare, făcută atât de Newton, cât și de Leibniz, care și-au bazat rezultatele pe lucrările anterioare ale lui Isaac Barrow, a fost cheia proliferării rezultatelor analitice după ce munca lor a devenit cunoscută. Teorema fundamentală oferă o metodă algebrică de calcul a multor integrale definite—fără a efectua procese limită—prin găsirea formulelor pentru antiderivative. Este, de asemenea, o soluție prototip a unei ecuații diferențiale. Ecuațiile diferențiale raportează o funcție necunoscută derivatelor sale și sunt omniprezente în științe.