limieten en infinitesimalen
Calculus wordt meestal ontwikkeld door te werken met zeer kleine hoeveelheden. Historisch gezien was de eerste methode om dit te doen door infinitesimalen. Dit zijn objecten die als reële getallen kunnen worden behandeld, maar die in zekere zin “oneindig klein”zijn. Bijvoorbeeld, een infinitesimaal getal kan groter zijn dan 0, maar minder dan elk getal in de reeks 1, 1/2, 1/3,… en dus minder dan elk positief reëel getal. Vanuit dit oogpunt is calculus een verzameling technieken voor het manipuleren van infinitesimalen. De symbolen d x {\displaystyle dx}

en d y {\displaystyle dy}

werden infinitesimaal geacht, en de afgeleide d y / d x {\displaystyle dy/dx}

was gewoon hun verhouding. de infinitesimale benadering viel in de 19e eeuw uit de gratie omdat het moeilijk was om de notie van een infinitesimale precies te maken. Echter, het concept werd nieuw leven ingeblazen in de 20e eeuw met de introductie van niet-standaard analyse en gladde infinitesimale analyse, die een solide basis voor de manipulatie van infinitesimalen.in de late 19e eeuw werden infinitesimalen binnen de academische wereld vervangen door de Epsilon, deltabenadering van grenzen. Limieten beschrijven de waarde van een functie bij een bepaalde input in termen van zijn waarden bij nabijgelegen inputs. Ze vangen kleinschalig gedrag in de context van het reële getalsysteem. In deze behandeling, calculus is een verzameling van technieken voor het manipuleren van bepaalde grenzen. Infinitesimalen worden vervangen door zeer kleine getallen, en het oneindig kleine gedrag van de functie wordt gevonden door het beperkende gedrag voor kleinere en kleinere getallen te nemen. Men dacht dat limieten een meer rigoureuze basis vormden voor calculus, en om deze reden werden ze de standaardbenadering gedurende de twintigste eeuw.
Differentiaalrekening

Differentiaalrekening is de studie van de definitie, eigenschappen en toepassingen van de afgeleide van een functie. Het proces van het vinden van de afgeleide wordt differentiatie genoemd. Gegeven een functie en een punt in het domein, is de afgeleide op dat punt een manier om het kleinschalige gedrag van de functie in de buurt van dat punt te coderen. Door de afgeleide van een functie op elk punt in zijn domein te vinden, is het mogelijk om een nieuwe functie te produceren, genaamd de afgeleide functie of gewoon de afgeleide van de oorspronkelijke functie. Formeel gezien is de afgeleide een lineaire operator die een functie als input neemt en een tweede functie als output produceert. Dit is abstracter dan veel van de processen die in de elementaire algebra worden bestudeerd, waar functies gewoonlijk een getal invoeren en een ander getal uitvoeren. Bijvoorbeeld, als de verdubbelfunctie de input drie krijgt, dan voert het zes uit, en als de squaring-functie de input drie krijgt, dan voert het negen uit. De afgeleide kan echter de squaring functie als input nemen. Dit betekent dat de afgeleide alle informatie van de squaring functie neemt – zoals dat twee wordt verzonden naar vier, drie wordt verzonden naar negen, vier wordt verzonden naar zestien, enzovoort-en deze informatie gebruikt om een andere functie te produceren. De functie die ontstaat door het afleiden van de squaring-functie blijkt de verdubbelfunctie te zijn.
in meer expliciete termen kan de” dubbelfunctie “worden aangeduid met g(x) = 2x en de” squaring-functie ” met f(x) = x2. De ” afgeleide “neemt nu de functie f(x), gedefinieerd door de uitdrukking” x2″, als een input, dat is alle informatie—zoals dat twee wordt verzonden naar vier, drie wordt verzonden naar negen, vier wordt verzonden naar zestien, enzovoort—en gebruikt deze informatie om een andere functie uit te voeren, de functie g(x) = 2x, zoals zal blijken.
het meest voorkomende symbool voor een afgeleide is een apostrofachtig teken dat priemgetal wordt genoemd. Zo wordt de afgeleide van een functie genaamd f aangeduid met f’, uitgesproken als “F priemgetal”. Bijvoorbeeld, als f ( x) = x2 de squaring functie is, dan is f'(x) = 2x de afgeleide (de verdubbelfunctie g van bovenaf). Deze notatie staat bekend als Lagrange ‘ s notatie.
als de input van de functie tijd voorstelt, dan vertegenwoordigt de afgeleide verandering met betrekking tot tijd. Bijvoorbeeld, als f een functie is die een tijd als input neemt en de positie van een bal op dat moment als output geeft, dan is de afgeleide van f hoe de positie in de tijd verandert, dat wil zeggen, het is de snelheid van de bal.
als een functie lineair is (dat wil zeggen, als de grafiek van de functie een rechte lijn is), dan kan de functie worden geschreven als y = mx + b, waarbij x de onafhankelijke variabele is, y de afhankelijke variabele is, b De y-ordinaat is, en:
m = rise run = change in y change in x = Δ y Δ x . {\displaystyle m={\frac {\text{rise}} {\text{run}}} = {\frac {{\text{change in}} y} {{\text{change in }}x}}={\frac {\Delta y} {\Delta x}}.}

Dit geeft een exacte waarde voor de helling van een rechte lijn. Als de grafiek van de functie echter geen rechte lijn is, dan varieert de verandering in y gedeeld door de verandering in x. Derivaten geven een exacte betekenis aan het begrip verandering in output ten opzichte van verandering in input. Om concreet te zijn, Laat f een functie zijn, en fix een punt a in het domein van f. (A, f(a)) is een punt op de grafiek van de functie. Als h een getal dicht bij nul is, dan is a + h een getal dicht bij a.daarom is (a + h, f(a + h)) dicht bij (a, f(a)). De helling tussen deze twee punten is
m = f − a + h) − f ( a) (a + h ) − A = f ( A + h) – f ( A) h . {\displaystyle m={\frac {f (a + h)-f(a)} {(A+h)-a}}={\frac {f(a+h) – f(a)} {h}}.}

deze uitdrukking wordt een verschil quotiënt genoemd. Een lijn door twee punten op een kromme wordt een secantlijn genoemd, dus m is de helling van de secantlijn tussen (a, f(a)) en (a + h, f(A + h)). De secant lijn is slechts een benadering van het gedrag van de functie op het punt a omdat het geen rekening houdt met wat er gebeurt tussen a en a + h. Het is niet mogelijk om het gedrag bij a te ontdekken door h op nul te zetten omdat dit zou vereisen delen door nul, wat niet gedefinieerd is. De afgeleide wordt gedefinieerd door de limiet te nemen als h neigt naar nul, wat betekent dat het het gedrag van f beschouwt voor alle kleine waarden van h en een consistente waarde extraheert voor het geval dat h gelijk is aan nul:
lim h → 0 f ( A + h ) − f ( a ) h . {\displaystyle \ lim _{h \ to 0}{f (A+h)-f(A) \over {h}}.}

Meetkundig is de afgeleide de helling van de raaklijn aan de grafiek van f bij a. de raaklijn is een limiet van secantlijnen net zoals de afgeleide een limiet is van verschilquotiënten. Om deze reden wordt de afgeleide ook wel de helling van de functie f.
Hier is een bijzonder voorbeeld, de afgeleide van de squaring functie bij de ingang 3. Zij f ( x) = x2 de squaring functie.

f ′ ( 3 ) = lim h → 0 ( 3 + h ) 2 − 3 2 h = lim h → 0 9 + 6 h + h 2 − 9 h = lim h → 0 6 h + h 2 h = lim h → 0 ( 6 + h ) = 6 {\displaystyle {\begin{aligned}f'(3)&=\lim _{h\to 0}{(3+h)^{2}-3^{2} \over {h}}\\&=\lim _{h\to 0}{9+6h+h^{2}-9 \over {h}}\\&=\lim _{h\to 0}{6h+h^{2} \over {h}}\\&=\lim _{h\to 0}(6+h)\\&=6\end{aligned}}}

De Helling van de raaklijn aan de squaring-functie op het punt (3, 9) is 6, dat wil zeggen, het gaat zes keer zo snel omhoog als het naar rechts gaat. Het zojuist beschreven limietproces kan worden uitgevoerd voor elk punt in het domein van de squaring functie. Dit definieert de afgeleide functie van de squaring functie of kortweg de afgeleide van de squaring functie. Een berekening zoals hierboven laat zien dat de afgeleide van de squaring-functie de verdubbelfunctie is.
Leibniz notatie
een veel voorkomende notatie, geïntroduceerd door Leibniz, voor de afgeleide in het voorbeeld hierboven is
y = x 2 d y d x = 2 x . {\displaystyle {\begin{aligned}y&=x^{2}\\{\frac {dy}{dx}}&=2x.\end{aligned}}}

in een benadering gebaseerd op limieten moet het symbool dy/dx niet worden geïnterpreteerd als het quotiënt van twee getallen, maar als een afkorting voor de hierboven berekende limiet. Leibniz wilde echter wel het quotiënt van twee infinitesimaal kleine getallen voorstellen, dy is de infinitesimaal kleine verandering in y veroorzaakt door een infinitesimaal kleine verandering DX toegepast op x. we kunnen ook denken aan d/dx als een differentiatieoperator, die een functie als input neemt en een andere functie, de afgeleide, als output geeft. Bijvoorbeeld:
d d x (x 2) = 2 x . {\displaystyle {\frac {d}{dx}} (x^{2})=2x.}

bij dit gebruik wordt de DX in de noemer gelezen als “met betrekking tot x”. Een ander voorbeeld van correcte notatie zou kunnen zijn:
g ( t ) = t 2 + 2 t + 4 d d t g ( t ) = 2 t + 2 {\displaystyle {\begin{aligned}g(t)=t^{2}+2t+4\\\\{d \over dt}g(t)=2t+2\end{aligned}}}

Zelfs als calculus is ontwikkeld met behulp van beperkingen in plaats infinitesimals, het is gebruikelijk om het manipuleren van symbolen zoals dx en dy, als waren zij met reële getallen; hoewel het mogelijk is om te voorkomen dat dergelijke manipulaties, ze zijn soms notationally handig zijn in het uiten van activiteiten zoals het totaal afgeleide.
integrale calculus
integrale calculus is de studie van de definities, eigenschappen en toepassingen van twee verwante concepten, de onbepaalde integraal en de definitieve integraal. Het proces van het vinden van de waarde van een integraal wordt integratie genoemd. In technische taal, integral calculus studies twee verwante lineaire operatoren.
De onbepaalde integraal, ook bekend als de primitieve integraal, is de inverse van de afgeleide. F is een onbepaalde integraal van f wanneer f een afgeleide is van F. (Dit gebruik van hoofdletters en kleine letters voor een functie en zijn onbepaalde integraal is gebruikelijk in de calculus.)
De definitieve integraal voert een functie in en geeft een getal uit, wat de algebraïsche som van gebieden tussen de grafiek van de input en de x-as geeft. De technische definitie van de definitieve integraal omvat de limiet van een som van gebieden van rechthoeken, een Riemann-som genoemd.
een motiverend voorbeeld is de afgelegde afstanden in een bepaalde tijd.
D I s T a n c e = S p e E D ⋅ T I m e {\displaystyle \mathrm {afstand} =\mathrm {snelheid} \cdot \mathrm {tijd} }

als de snelheid constant is, is alleen vermenigvuldiging nodig, maar als de snelheid verandert, een krachtigere methode om de afstand te vinden is noodzakelijk. Een van deze methoden is om de afgelegde afstand te benaderen door de tijd op te splitsen in vele korte tijdsintervallen, vervolgens de in elk interval verstreken tijd te vermenigvuldigen met een van de snelheden in dat interval, en dan de som (een Riemann-som) te nemen van de geschatte afstand die in elk interval wordt afgelegd. Het basisidee is dat als slechts een korte tijd verstrijkt, dan zal de snelheid min of meer hetzelfde blijven. Een Riemann-som geeft echter slechts een benadering van de afgelegde afstand. We moeten de limiet van al die Riemann-sommen nemen om de exacte afgelegde afstand te vinden.
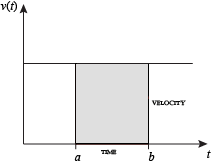

wanneer de snelheid constant is, kan de totale afgelegde afstand over het gegeven tijdsinterval worden berekend door de snelheid en de tijd te vermenigvuldigen. Bijvoorbeeld, het reizen van een constante 50 km / u gedurende 3 uur resulteert in een totale afstand van 150 mijl. In het diagram links, wanneer constante snelheid en tijd worden weergegeven, vormen deze twee waarden een rechthoek met hoogte gelijk aan de snelheid en breedte gelijk aan de verstreken tijd. Daarom berekent het product van snelheid en tijd ook de rechthoekige oppervlakte onder de (constante) snelheidscurve. Deze verbinding tussen het gebied onder een curve en de afgelegde afstand kan worden uitgebreid tot elk onregelmatig gevormd gebied met een fluctuerende snelheid over een bepaalde periode. Als f (x) in het diagram rechts de snelheid voorstelt zoals deze in de tijd varieert, is de afgelegde afstand (tussen de tijden die worden weergegeven door a en b) de oppervlakte van het gearceerde gebied s.
om dat gebied te benaderen, zou een intuïtieve methode zijn om de afstand tussen A en b te verdelen in een aantal gelijke segmenten, de lengte van elk segment dat wordt weergegeven door het symbool Δx. Voor elk klein segment kunnen we één waarde van de functie f(x) kiezen. Noem die waarde h. dan geeft de oppervlakte van de rechthoek met basis Δx en hoogte h de afstand (tijd Δx vermenigvuldigd met snelheid h) afgelegd in dat segment. Geassocieerd met elk segment is de gemiddelde waarde van de functie erboven, f(x) = h. de som van al deze rechthoeken geeft een benadering van het gebied tussen de as en de kromme, dat is een benadering van de totale afgelegde afstand. Een kleinere waarde voor Δx geeft meer rechthoeken en in de meeste gevallen een betere benadering, maar voor een exact antwoord moeten we een limiet nemen als Δx nadert tot nul.
Het symbool van integratie is ∫ {\displaystyle \int}

, een langgerekte S (De S staat voor “Som”). De definitieve integraal wordt geschreven als: ∫ a b f (x ) d x . {\displaystyle \ int _{a}^{b}f (x)\, dx.}

en wordt gelezen “de integraal van a naar b van f-van-x met betrekking tot x.” de Leibniz-notatie dx is bedoeld om te suggereren het gebied onder de kromme te verdelen in een oneindig aantal rechthoeken, zodat hun breedte Δx de infinitesimaal kleine dx wordt. In een formulering van de calculus op basis van limieten moet de notatie
a a b ⋯ D x {\displaystyle \int _{a}^{b}\cdots\, dx}

worden begrepen als een operator die een functie als invoer neemt en een getal, het gebied, als uitvoer geeft. Het eindigende verschil, dx, is geen getal en wordt niet vermenigvuldigd met f (x), hoewel het, als herinnering aan de Δx-grensdefinitie, als zodanig kan worden behandeld in symbolische manipulaties van de integraal. Formeel geeft het differentieel de variabele aan waarover de functie is geïntegreerd en dient het als sluitbeugel voor de integratieoperator.
De onbepaalde integraal, of primitief, wordt geschreven:
∫ f (x) d x . {\displaystyle \ int f (x)\, dx.}

functies die alleen verschillen met een constante hebben dezelfde afgeleide, en het kan worden aangetoond dat de primitieve functie van een gegeven functie eigenlijk een familie van functies is die alleen verschillen met een constante. Aangezien de afgeleide van de functie y = x2 + C, waarbij C een constante is, y’ = 2x is, wordt de primitieve van de laatste gegeven door:
2 2 x d x = x 2 + C . {\displaystyle \ int 2x\, dx = x^{2} + C.}

De niet-gespecificeerde constante C aanwezig in de onbepaalde integraal of primitief staat bekend als de constante van integratie.
fundamentele stelling
de fundamentele stelling van calculus stelt dat differentiatie en integratie inverse operaties zijn. Meer precies, het relateert de waarden van primitieven aan bepaalde integralen. Omdat het meestal gemakkelijker is om een primitief te berekenen dan om de definitie van een bepaalde integraal toe te passen, biedt de fundamentele stelling van calculus een praktische manier om bepaalde integralen te berekenen. Het kan ook worden geïnterpreteerd als een precieze verklaring van het feit dat differentiatie het omgekeerde van integratie is.
de fundamentele stelling van calculusstaten: Als een functie F continu is op het interval en als F een functie is waarvan de afgeleide f is op het interval (a, b), dan
∫ a b f ( x ) d x = F ( b ) − F ( a ) . {\displaystyle \ int _{a}^{b}f (x)\, dx = F(b)-F (a).}

Bovendien, voor elke X in het interval (a, b),
d d x ∫ A x f ( t ) d t = f ( x ) . {\displaystyle {\frac {d}{dx}}\int _{a}^{x}f (t)\, dt = f (x).}

Deze realisatie, gemaakt door zowel Newton als Leibniz, die hun resultaten baseerden op eerder werk van Isaac Barrow, was de sleutel tot de proliferatie van analytische resultaten nadat hun werk bekend werd. De fundamentele stelling biedt een algebraïsche methode voor het berekenen van veel bepaalde integralen—zonder limietprocessen uit te voeren—door formules voor primitieven te vinden. Het is ook een prototype oplossing van een differentiaalvergelijking. Differentiaalvergelijkingen relateren een onbekende functie aan zijn afgeleiden, en zijn alomtegenwoordig in de wetenschappen.