Nylig tenkte jeg på ulike begrunnelser for definisjonen av 0! (factorial av null) som er
$$0!=1$ $
den antatte verdien av 1 kan virke ganske åpenbar hvis du vurderer rekursiv formel. Men det tilfredsstilte meg ikke «matematisk». Derfor bestemte jeg meg for å skrive disse få setningene. Jeg vil gi motivasjoner for de mindre avanserte, men det vil også være motivasjoner for litt flere innsidere.
⭐ ️ faktoriell I skalar Kalkulator

⭐ ️ faktoriell og Gjentakelse
for heltall n>0 faktoriell er definert som følger
$$n!=n \ times (n-1) \ times (n-2)\times \ldots \times 2\times 1$$
Med letthet kan du se at under rekursiv formel følger
$ $ n!= n \ ganger (n-1)!$$
$ $ 1!=1$ $
⭐ ️ 0! = 1-motivasjon basert på tilbakefall
Liten transformasjon av
$$n!= n \ ganger (n-1)!$$
gir
$$(n-1)!= \ frac{n!}{n}$ $
Erstatte n = 1
$$(1-1)!= \frac{1!}{1}$$
$$0!=1!= 1$$
denne forklaringen, selv om den er enkel, gir ikke (etter min mening) dyp nok forståelse av «hvorfor dette burde være det beste alternativet».
⭐ ️ factorial n! (permutasjoner)
la oss anta at vi har et sett som inneholder n elementer
$$\{1,2,\ldots,n\}$$
nå la»s telle mulig bestilling av elementer er dette settet
- n måter å velge første element (fordi vi har hele settet tilgjengelig)
- n-1 måter å velge andre element (fordi den første allerede var valgt, er det n-1 venstre)
- n-2 måter å velge tredje element (fordi De to allerede var valgt, er det n-2 igjen)
- …
- n – (k-1) måter å velge elementnummer k (fordi k-1 allerede var valgt, forblir n- (k-1))
- 2 måter å velge elementnummer n-1 (fordi n-2 ble valgt, fortsatt 2 forblir)
- 1 måte å velge elementnummer n (fordi n-1 ble valgt, forblir bare en)
Til slutt, teller alle mulige måter, får vi
$$n\ganger (n-1)\ganger (n-2)\ganger \ldots \ganger 2\ganger 1=n!$ $
Konklusjon: Faktoriell av n teller antall permutasjon av et sett som inneholder n elementer.
⭐ ️ k-permutasjoner av n noen ganger kalt partielle permutasjoner eller variasjoner
K-permutasjonene av n er de forskjellige ordnede arrangementene av et k-element delsett av et n-sett. Antallet slike k-permutasjoner av n er
$$P_k^n = n \ ganger (n-1)\ganger (n-2) \ ganger \ ldots \ ganger \ bigg(n-(k-1)\bigg) = \frac{n!{(n-k)!} $$
det er lett å se at n-permutasjon av n er en permutasjon, så
$$P_n^n=n!$ $
$ $ n! = \ frac{n!{(n-n)!} = \frac{n!}{0!} $ $
neste innsikt hvorfor 0!=1 er den riktige definisjonen kommer fra det for noen n > 0 vi burde ha
$ $ 0! \ ganger n! = n!$ $
⭐ ️ funksjon som et sett kartlegging

funksjon
$ $f:A\to B$ $
Funksjon f : En → B, der for hver en ∈ A det er f(a) = b ∈ B, definerer forholdet mellom elementene a og b. vi kan si at elementene a ∈ A og b ∈ B er i forhold «f» hvis og bare hvis f (a) = b.
⭐ ️ funksjon som en delmengde av kartesisk Produkt
funksjon Er en binær relasjon, noe som betyr at funksjonen kan uttrykkes som en delmengde av et kartesisk Produkt.
$$(a,b)\i f \subseteq A\ganger B \iff f(a)=b$$
⭐ ️ injeksjonsfunksjon

injektiv funksjon er en funksjon som bevarer distinkthet: den tilordner aldri distinkte elementer av domenet Til det samme elementet i kodomenet. Kort tid
$$x\neq y \Rightarrow f(x) \neq f(y)$$
⭐ ️ surjektiv Funksjon

en funksjon f er surjektiv (eller på) hvis for hvert element B I Codomain, er det minst ett element a i domenet slik at f(a)=b . Det er ikke nødvendig at x er unik.
$ $ f:A\til B$$
$${\stor \displaystyle\forall_{b \i b} \quad\displaystyle\exists_{a\i a}\quad}f(a)=b$$
⭐ ️ bijektiv Funksjon

bijektiv funksjon, eller en-til-en korrespondanse, er en funksjon der Hvert Element i ett sett er parret med nøyaktig ett element i det andre settet, og hvert element i det andre settet Er Parret Med Nøyaktig Ett element i det første settet. Det er ingen uparede elementer.
i matematiske termer er en bijektiv funksjon både injektiv og surjektiv kartlegging av et sett A Til et sett B.
⭐ ️ bijektiv Funksjon vs permutasjon
permutasjon er en funksjon som returnerer rekkefølgen til et sett, dvs.hvis vi vurderer n-elementet sett {1, 2,…, n} da vil permutasjon være en funksjon
$$p:\{1, 2,…, n\}\til\{1, 2,…, n\}$$
tilfredsstiller bijektiv funksjonsbetingelsen.
ved å spørre om antall permutasjoner kan vi også spørre om antall forskjellige bijections fra et gitt sett i seg selv.
⭐ ️ tom Funksjon
En Tom funksjon er hver funksjon hvis domene er et tomt sett.
$$f:\emptyset\to b$$
den tomme funksjonen «chart» er et tomt sett, da Det Kartesiske produktet av domene og codomain er tomt.
$$\emptyset\times B = \emptyset$$
den tomme funksjonen bevarer distinkthet (er injektiv), fordi i domenet (et tomt sett) er det ikke to forskjellige elementer for hvilke verdien av funksjonen er lik.
⭐ ️ Et Spesielt tilfelle av en tom funksjon
la oss analysere funksjonen som kartlegger tomt til tomt sett
$ $f:en slik funksjon er en bijection fordi den er injektiv funksjon (som vist ovenfor) og det er ikke noe element i codomain (codomain er et tomt sett) som ikke er i forhold til elementene i domenet.
Vær oppmerksom på at det er akkurat en slik bijection, som er et resultat av at funksjonen er en delmengde Av Det Kartesiske produktet av domene og codomain. I dette tilfellet er dette bare ett mulig sett.
$ $ f:\emptyset\to\emptyset$$
$$\emptyset\times \emptyset = \ emptyset$$
det tomme settet har nøyaktig en delmengde – som er det tomme settet – slik at en slik bijeksjon er unikt definert.
⭐ ️ 0! = 1 vs Tom funksjon
jeg skrev over at antall permutasjoner av et n-elementsett er lik antall distinkte bijektive funksjoner fra dette settet i seg selv.
Følgende-permutasjonen av 0-elementsettet tilsvarer bijeksjonen fra et tomt sett til det tomme settet/
det spesielle tilfellet med tom funksjon er bare 1 – og jeg presenterte beviset på at det bare finnes en slik funksjon 🙂
Ganske dyp innsikt hvorfor 0! bør være 1.
⭐ ️ Gammafunksjonen
i Matematikk er gammafunksjonen en av utvidelsene av faktorialfunksjonen med argumentet skiftet ned med 1, til ekte og komplekse tall.
$$\Gamma(z)=\displaystyle\int_0^{+\infty}t^{z-1}e^{-t}dt$$
etter integrasjon av deler får vi den rekursive formelen
$$\Gamma(z+1)=z\cdot\Gamma(z)$$
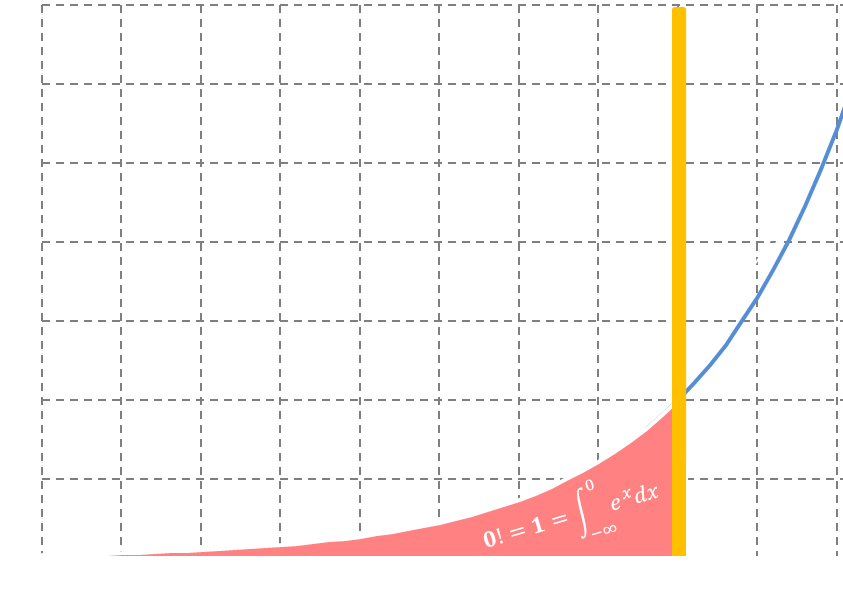
La oss se verdien av
$$\Gamma(1)=?$$
$ $ \Gamma(1)=\displaystyle\int_0^{+\infty}e^{-t}dt=\displaystyle\int_{-\infty}^{0}e^{t}dt$$
Følger
$$\Gamma (n+1)=n!$$
$ $ 0! = \Gamma(1) = 1$$
⭐️ Scalar support for the Gamma function

Functions in Scalar Calculator, that support Gamma special function
- Gamma(x) – Gamma special function Γ(s)
- sgnGamma(x) – Signum of Gamma special function, Γ(s)
- logGamma(x) – Log Gamma special function, lnΓ(s)
- diGamma(x) – Digamma function as the logarithmic derivative of the Gamma special function, ψ(x)
- GammaL(s,x) – Lower incomplete gamma special function, γ(s,x)
- GammaU(s,x) – Upper incomplete Gamma special function, Γ(s,x)
- GammaP(s,x) , GammaRegL(s,x) – Lower regularized P gamma special function, P(s,x)
- GammaQ(s,x), GammaRegU(s,x) – Upper regularized Q Gamma special function, Q(s,x)
Gamma function chart

Gamma function vs Factorial chart

⭐ ️ nummer E Og faktoriell relasjon
basert på taylor-Seriens utvidelse av e^x er det lett å vise at
$$e=\displaystyle\sum_{n=0}^\infty\frac{1}{n!} = \frac{1}{0!} + \ frac{1}{1!} + \ frac{1}{2!} + \ frac{1}{3!}+\ldots$$
Sequence convergence

This is fascinating, as it shows even stronger relation of factorial to e
Thanks for reading! All the best 🙂