Grenser og infinitesimals
Kalkulus er vanligvis utviklet ved å arbeide med svært små mengder. Historisk sett var den første metoden for å gjøre det ved uendelige. Dette er objekter som kan behandles som ekte tall, men som på en eller annen måte er «uendelig små». For eksempel kan et uendelig tall være større enn 0, men mindre enn noe tall i sekvensen 1, 1/2, 1/3,… og dermed mindre enn noe positivt reelt tall. Fra dette synspunkt er kalkulator en samling teknikker for å manipulere infinitesimaler. Symbolene d x {\displaystyle dx}

og d y {\displaystyle dy}

ble tatt for å være infinitesimale, og den deriverte d y / d x {\displaystyle dy/dx}

var ganske enkelt deres forhold. den uendelige tilnærmingen falt i unåde i det 19. århundre fordi det var vanskelig å gjøre forestillingen om en uendelig presis. Konseptet ble imidlertid gjenopplivet i det 20. århundre med innføring av ikke-standardanalyse og jevn uendelig analyse, noe som ga solid grunnlag for manipulering av uendelige.på slutten av det 19. århundre ble infinitesimals erstattet innen akademia av epsilon, delta approach to limits. Grenser beskriver verdien av en funksjon ved en bestemt inngang i form av dens verdier ved nærliggende innganger. De fanger småskala oppførsel i sammenheng med det reelle tallsystemet. I denne behandlingen er kalkulator en samling teknikker for å manipulere visse grenser. Infinitesimals blir erstattet av svært små tall, og uendelig liten oppførsel av funksjonen er funnet ved å ta begrensende oppførsel for mindre og mindre tall. Grenser ble antatt å gi en strengere grunnlag for kalkulus, og av denne grunn ble de standard tilnærming i løpet av det tjuende århundre.
Differensialkalkulator

i mer eksplisitte termer kan «doblingsfunksjonen» betegnes med g (x) = 2x og «kvadreringsfunksjonen» med f (x) = x2. «Derivatet» tar nå funksjonen f (x), definert av uttrykket «x2», som en inngang, det vil si all informasjon—for eksempel at to sendes til fire, tre sendes til ni, fire sendes til seksten, og så videre—og bruker denne informasjonen til å utføre en annen funksjon, funksjonen g(x) = 2x, som det vil vise seg.
det vanligste symbolet for et derivat er et apostrof-lignende merke kalt prime. Dermed er derivatet av en funksjon kalt f betegnet med f’, uttalt «f prime». For eksempel, hvis f (x) = x2 er kvadreringsfunksjonen, er f'(x) = 2x dens derivat (doblingsfunksjonen g ovenfra). Denne notasjonen er kjent som Lagrange notasjon.
hvis inngangen til funksjonen representerer tid, representerer derivatet endring med hensyn til tid. For eksempel, hvis f er en funksjon som tar en tid som inngang og gir posisjonen til en ball på den tiden som utgang, så er derivatet av f hvordan posisjonen endrer seg i tid, det vil si at det er ballens hastighet.
hvis en funksjon er lineær( det vil si hvis grafen til funksjonen er en rett linje), kan funksjonen skrives som y = mx + b, der x er den uavhengige variabelen, y er den avhengige variabelen, b er y-avskjæringen, og:
m = stigning = endring i y endring i x = Δ y Δ x . {\displaystyle m={\frac {\text{rise}} {\text{run}}}={\frac {{\text{change in }}y}{{\text{change in}} {{\text {change in}} x}}={\Frac {\Delta y} {\Delta x}}.}

dette gir en nøyaktig verdi for hellingen til en rett linje. Hvis grafen til funksjonen ikke er en rett linje, varierer endringen i y dividert med endringen i x. Derivater gir en nøyaktig mening til begrepet endring i utgang med hensyn til endring i inngang. For å være konkret, la f være en funksjon, og fikse et punkt a i domenet til f. (a, f (a)) er et punkt på grafen til funksjonen. Hvis h er et tall nær null, er a + h et tall nær a.Derfor er (a + h, f(a + h)) nær (a, f(a)). Hellingen mellom disse to punktene er
m = f ( a + h ) − f ( a ) ( a + h ) − a = f ( a + h ) − f ( a ) h . {\displaystyle m={\frac {f (a + h) – f (a)} {(a+h) – a}}={\frac {f (a+h) – f (a)}{h}}.}

dette uttrykket kalles en forskjellskvotient. En linje gjennom to punkter på en kurve kalles en sekantlinje, så m er skråningen av sekantlinjen mellom (a, f (a)) og(a + h, f (a + h)). Secantlinjen er bare en tilnærming til funksjonens oppførsel ved punkt a fordi den ikke tar hensyn til hva som skjer mellom a og a + h. Det er ikke mulig å oppdage oppførselen ved a ved å sette h til null fordi dette ville kreve å dele med null, som er udefinert. Derivatet er definert ved å ta grensen som h har en tendens til null, noe som betyr at den vurderer oppførselen til f for alle små verdier av h og trekker ut en konsistent verdi for saken når h er lik null:
lim h → 0 f ( a + h ) − f ( a ) h . {\displaystyle \ lim _ {h\til 0}{f (a + h) – f (a) \over {h}}.}

Her er et spesielt eksempel, derivatet av kvadreringsfunksjonen ved inngangen 3. La f (x) = x2 være kvadreringsfunksjonen.

f ′ ( 3 ) = lim h → 0 ( 3 + h ) 2 − 3 2 h = lim h → 0 9 + 6 h + h 2 − 9 h = lim h → 0 6 h + h 2 h = lim h → 0 ( 6 + h ) = 6 {\displaystyle {\begin{aligned}f'(3)&=\lim _{h\to 0}{(3+h)^{2}-3^{2} \over {h}}\\&=\lim _{h\to 0}{9+6h+h^{2}-9 \over {h}}\\&=\lim _{h\to 0}{6h+h^{2} \over {h}}\\&=\lim _{h\to 0}(6+h)\\&=6\end{aligned}}}

hellingen til tangentlinjen til kvadreringsfunksjonen ved punktet (3, 9) er 6, det vil si, det går opp seks ganger så fort som det går til høyre. Grenseprosessen som nettopp er beskrevet, kan utføres for ethvert punkt i domenet til kvadreringsfunksjonen. Dette definerer den deriverte funksjonen av kvadreringsfunksjonen eller bare den deriverte av kvadreringsfunksjonen for kort. En beregning som ligner den ovenfor viser at derivatet av kvadreringsfunksjonen er doblingsfunksjonen.
Leibniz notasjon
en felles notasjon, introdusert Av Leibniz, for derivatet i eksemplet ovenfor er
y = x 2 d y d x = 2 x . {\displaystyle {\begin{aligned}y&=x^{2}\\{\frac {dy}{dx}}&=2x.\end{aligned}}}

i en tilnærming basert på grenser skal symbolet dy/dx tolkes ikke som kvotienten av to tall, men som en forkortelse for grensen beregnet ovenfor. Leibniz hadde imidlertid til hensikt å representere kvotienten av to uendelig små tall, dy er den uendelig små endringen i y forårsaket av en uendelig liten endring dx brukt på x. Vi kan også tenke på d / dx som en differensieringsoperatør, som tar en funksjon som inngang og gir en annen funksjon, derivatet, som utgangen. For eksempel:
d d x (x 2) = 2 x . {\displaystyle {\frac {d}{dx}} (x^{2}) = 2x.}

i denne bruken leses dx i nevnen som «med hensyn til x». Et annet eksempel på korrekt notasjon kan være:
g ( t ) = t 2 + 2 t + 4 d d t g ( t ) = 2 t + 2 {\displaystyle {\begin{aligned}g(t)=t^{2}+2t+4\\\{d\over dt}g(t)=2t+2 \end{aligned}}}

selv når kalkulus er utviklet ved hjelp av grenser i stedet for uendelige, er det vanlig å manipulere symboler som dx og dy som om de var reelle tall; selv om det er mulig å unngå slike manipulasjoner, er de noen ganger notasjonelt praktiske i å uttrykke operasjoner som totalderivatet.
Integralregning
Integralregning er studiet av definisjonene, egenskapene og anvendelsene av to beslektede begreper, det ubestemte integralet og det bestemte integralet. Prosessen med å finne verdien av et integral kalles integrasjon. I teknisk språk studerer integral kalkulator to relaterte lineære operatører.
ubestemt integral, også kjent som antiderivativ, er den inverse operasjonen til derivatet. F er et ubestemt integral av f når f er et derivat Av F. (Denne bruken av små og store bokstaver for en funksjon og dens ubestemte integral er vanlig i kalkulator.)
den bestemte integral innganger en funksjon og utganger et tall, som gir den algebraiske summen av områder mellom grafen av inngangen og x-aksen. Den tekniske definisjonen av det bestemte integralet innebærer grensen for en sum av områder av rektangler, kalt En Riemannsum.
et motiverende eksempel er avstandene reist i en gitt tid.

hvis hastigheten er konstant, er det bare nødvendig med multiplikasjon, men hvis hastigheten endres, er det nødvendig med en kraftigere metode for å finne avstanden. En slik metode er å tilnærme avstanden som er reist ved å bryte opp tiden i mange korte tidsintervaller, deretter multiplisere tiden som er gått i hvert intervall med en av hastighetene i det intervallet, og deretter ta summen (En Riemannsum) av den omtrentlige avstanden som er reist i hvert intervall. Den grunnleggende ideen er at hvis bare kort tid går, vil hastigheten forbli mer eller mindre den samme. Imidlertid gir En Riemann sum bare en tilnærming av avstanden som er reist. Vi må ta grensen for Alle Slike Riemann-summer for å finne den nøyaktige avstanden som er reist.
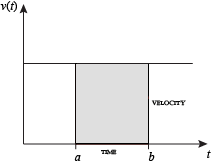

når hastigheten er konstant, kan den totale avstanden som er reist over det angitte tidsintervallet beregnes ved å multiplisere hastighet og tid. For eksempel, reiser en jevn 50 mph i 3 timer resulterer i en total avstand på 150 miles. I diagrammet til venstre, når konstant hastighet og tid er grafert, danner disse to verdiene et rektangel med høyde lik hastigheten og bredden lik tiden som er gått. Derfor beregner produktet av hastighet og tid også det rektangulære området under (konstant) hastighetskurven. Denne forbindelsen mellom området under en kurve og distanse kan utvides til en hvilken som helst uregelmessig formet region som viser en svingende hastighet over en gitt tidsperiode. Hvis f (x) i diagrammet til høyre representerer hastighet ettersom den varierer over tid, er avstanden som er reist (mellom tider representert av a og b) området for det skyggefulle området s.
for å tilnærme dette området, vil en intuitiv metode være å dele opp avstanden mellom a og b i et antall like segmenter, lengden på hvert segment representert av symbolet Δ. For hvert lite segment kan vi velge en verdi av funksjonen f (x). Kall den verdien h. da arealet av rektangelet med Base Δ og høyde h gir avstanden (Tid Δ multiplisert med hastighet h) reist i det segmentet. Tilknyttet hvert segment er gjennomsnittsverdien av funksjonen over den, f (x) = h. summen av alle slike rektangler gir en tilnærming av området mellom aksen og kurven, som er en tilnærming av den totale avstanden som er reist. En mindre verdi for Δ vil gi flere rektangler og i de fleste tilfeller en bedre tilnærming, men for et eksakt svar må vi ta en grense som Δ nærmer seg null.
symbolet for integrasjon er ∫ {\displaystyle \int}

, en langstrakt S (s står for «sum»). Det bestemte integralet er skrevet som: ∫ a b f (x) d x . {\displaystyle \ int _{a}^{b}f (x)\, dx.}

og leses «integralet fra a til b av f-of-x med hensyn til x.» Leibniz-notasjonen dx er ment å foreslå å dele området under kurven i et uendelig antall rektangler, slik at deres bredde Δ blir den uendelig små dx. I en formulering av kalkulatoren basert på grenser, skal notasjonen
∫ a b ⋯ d x {\displaystyle \ int _{a}^{b} \ cdots \, dx}

forstås som en operatør som tar en funksjon som inngang og gir et tall, området, som en utgang. Termineringsdifferensialet, dx, er ikke et tall, og blir ikke multiplisert med f(x), selv om det, som en påminnelse om Begrensningsdefinisjonen For Δ, kan behandles som sådan i symbolske manipulasjoner av integralet. Formelt angir differensialet variabelen over hvilken funksjonen er integrert og fungerer som en lukkebrakett for integrasjonsoperatøren.
ubestemt integral, eller antiderivativ, er skrevet:
∫ f ( x) d x . {\displaystyle \ int f (x)\, dx.}

Funksjoner som varierer med bare en konstant, har samme derivat, og Det kan vises at antideriveringen av en gitt funksjon faktisk er en familie av funksjoner som bare varierer med en konstant. Siden derivatet av funksjonen y = x2 + C, Hvor C er en hvilken som helst konstant, er y ‘ = 2x, er antideriveringen av sistnevnte gitt ved:
∫ 2 x d x = x 2 + C . {\displaystyle \ int 2x\, dx=x^{2} + C.}

den uspesifiserte konstanten C tilstede i ubestemt integral eller antiderivativ er kjent som integrasjonskonstanten.
Fundamental theorem
the fundamental theorem of calculus sier at differensiering og integrasjon er inverse operasjoner. Nærmere bestemt gjelder det verdiene av antideriver til bestemte integraler. Fordi det vanligvis er lettere å beregne et antideriveringsmiddel enn å anvende definisjonen av et bestemt integral, gir fundamental theorem of calculus en praktisk måte å beregne bestemte integraler på. Det kan også tolkes som en presis uttalelse av det faktum at differensiering er den inverse av integrasjon.
den grunnleggende teorem av kalkulus stater: Hvis en funksjon f er kontinuerlig på intervallet Og Hvis F Er en funksjon hvis derivat er f på intervallet (a, b), så
∫ a b f ( x ) d x = F ( b ) − F ( a ) . {\displaystyle \ int _{a}^{b}f (x)\, dx=F (b) – F (a).

videre, for hver x i intervallet (a, b),
d d x ∫ a x f (t ) d t = f (x). {\displaystyle {\frac{d} {dx}}\int _{a}^{x}f(t)\, dt=f(x).
