Limiti e infinitesimi
Il calcolo viene solitamente sviluppato lavorando con quantità molto piccole. Storicamente, il primo metodo per farlo era infinitesimale. Questi sono oggetti che possono essere trattati come numeri reali ma che sono, in un certo senso, “infinitamente piccoli”. Ad esempio, un numero infinitesimale potrebbe essere maggiore di 0, ma inferiore a qualsiasi numero nella sequenza 1, 1/2, 1/3,… e quindi meno di qualsiasi numero reale positivo. Da questo punto di vista, il calcolo è una raccolta di tecniche per manipolare gli infinitesimi. I simboli d x {\displaystyle dx}

e d y {\displaystyle dy}

sono stati presi da infinitesimale, e la derivata d y / d x {\displaystyle dy/dx}

era semplicemente il loro rapporto.
L’approccio infinitesimale cadde in disgrazia nel 19 ° secolo perché era difficile rendere precisa la nozione di un infinitesimo. Tuttavia, il concetto è stato ripreso nel 20 ° secolo con l’introduzione di analisi non standard e analisi infinitesimale liscia, che ha fornito solide basi per la manipolazione degli infinitesimi.
Alla fine del 19 ° secolo, gli infinitesimali furono sostituiti all’interno del mondo accademico dall’approccio epsilon, delta ai limiti. I limiti descrivono il valore di una funzione in un determinato input in termini di valori in ingressi vicini. Catturano il comportamento su piccola scala nel contesto del sistema di numeri reali. In questo trattamento, il calcolo è una raccolta di tecniche per manipolare determinati limiti. Gli infinitesimi vengono sostituiti da numeri molto piccoli e il comportamento infinitamente piccolo della funzione viene trovato prendendo il comportamento limitante per numeri sempre più piccoli. I limiti sono stati pensati per fornire una base più rigorosa per il calcolo, e per questo motivo sono diventati l’approccio standard durante il ventesimo secolo.
Calcolo differenziale

Il calcolo differenziale è lo studio della definizione, delle proprietà e delle applicazioni della derivata di una funzione. Il processo di ricerca del derivato è chiamato differenziazione. Data una funzione e un punto nel dominio, la derivata in quel punto è un modo di codificare il comportamento su piccola scala della funzione vicino a quel punto. Trovando la derivata di una funzione in ogni punto del suo dominio, è possibile produrre una nuova funzione, chiamata funzione derivata o solo la derivata della funzione originale. In termini formali, la derivata è un operatore lineare che prende una funzione come suo input e produce una seconda funzione come suo output. Questo è più astratto di molti dei processi studiati in algebra elementare, dove le funzioni di solito immettono un numero e producono un altro numero. Ad esempio, se alla funzione di raddoppio viene dato l’ingresso tre, allora ne emette sei, e se alla funzione di quadratura viene dato l’ingresso tre, allora emette nove. La derivata, tuttavia, può prendere la funzione di quadratura come input. Ciò significa che la derivata prende tutte le informazioni della funzione di quadratura—come ad esempio che due viene inviato a quattro, tre viene inviato a nove, quattro viene inviato a sedici, e così via—e utilizza queste informazioni per produrre un’altra funzione. La funzione prodotta derivando la funzione di quadratura risulta essere la funzione di raddoppio.
In termini più espliciti la “funzione di raddoppio” può essere indicata con g(x) = 2x e la “funzione di quadratura” con f(x) = x2. La “derivata” ora prende la funzione f(x), definita dall’espressione “x2”, come input, cioè tutte le informazioni—ad esempio che due vengono inviate a quattro, tre vengono inviate a nove, quattro vengono inviate a sedici e così via—e usa queste informazioni per produrre un’altra funzione, la funzione g (x) = 2x, come risulterà.
Il simbolo più comune per una derivata è un segno simile all’apostrofo chiamato primo. Pertanto, la derivata di una funzione chiamata f è indicata da f’, pronunciata “f prime”. Ad esempio, se f(x) = x2 è la funzione di quadratura, allora f'(x) = 2x è la sua derivata (la funzione di raddoppio g dall’alto). Questa notazione è nota come notazione di Lagrange.
Se l’input della funzione rappresenta il tempo, la derivata rappresenta il cambiamento rispetto al tempo. Ad esempio, se f è una funzione che richiede un tempo come input e fornisce la posizione di una palla in quel momento come output, allora la derivata di f è come la posizione sta cambiando nel tempo, cioè è la velocità della palla.
Se una funzione è lineare (cioè, se il grafico della funzione è una linea retta), allora la funzione può essere scritta come y = mx + b, dove x è la variabile indipendente, y è la variabile dipendente, b è l’intercetta y e:
m = rise run = change in y change in x = Δ y Δ x . Il nostro sito utilizza cookie tecnici e di terze parti per migliorare la tua esperienza di navigazione.}

Questo dà un valore esatto per la pendenza di una retta. Se il grafico della funzione non è una linea retta, tuttavia, il cambiamento in y diviso per il cambiamento in x varia. Le derivate danno un significato esatto alla nozione di cambiamento nell’output rispetto al cambiamento nell’input. Per essere concreto, sia f una funzione e fissa un punto a nel dominio di f. (a, f(a)) è un punto sul grafico della funzione. Se h è un numero vicino allo zero, allora a + h è un numero vicino ad a. Pertanto, (a + h, f (a + h)) è vicino a(a, f (a)). La pendenza tra questi due punti è
m = f − a + h) − f ( a) (a + h ) − a = f ( a + h) – f ( a) h . Il nostro sito utilizza cookie tecnici e di terze parti per migliorare la tua esperienza di navigazione. il nostro sito utilizza cookie tecnici e di terze parti per migliorare la tua esperienza di navigazione.
Questa espressione è chiamata quoziente di differenza. Una linea attraverso due punti su una curva è chiamata linea secante, quindi m è la pendenza della linea secante tra (a, f(a)) e (a + h, f(a + h)). La linea secante è solo un’approssimazione al comportamento della funzione nel punto a perché non tiene conto di ciò che accade tra a e a + h. Non è possibile scoprire il comportamento in a impostando h su zero perché ciò richiederebbe la divisione per zero, che non è definita. La derivata è definita prendendo il limite come h tende a zero, il che significa che considera il comportamento di f per tutti i piccoli valori di h ed estrae un valore coerente per il caso in cui h è uguale a zero:
lim h → 0 f ( a + h ) − f ( a ) h . {\displaystyle \ lim _ {h \ a 0}{f(a + h) – f (a) \ sopra {h}}. Non ci sono problemi con il sistema operativo.
Geometricamente, la derivata è la pendenza della linea tangente al grafico di f ad a. La linea tangente è un limite di linee secanti proprio come la derivata è un limite di quozienti di differenza. Per questo motivo, la derivata è talvolta chiamata la pendenza della funzione f.
Ecco un esempio particolare, la derivata della funzione di quadratura all’ingresso 3. Sia f ( x) = x2 la funzione di quadratura.

f ′ ( 3 ) = lim h → 0 ( 3 + h ) 2 − 3 2 h = lim h → 0 9 + 6 h + h 2 − 9 h = lim h → 0 6 h + h 2 h = lim h → 0 ( 6 + h ) = 6 {\displaystyle {\begin{aligned}f'(3)&=\lim _{h\to 0}{(3+h)^{2}-3^{2} \over {h}}\\&=\lim _{h\to 0}{9+6h+h^{2}-9 \over {h}}\\&=\lim _{h\to 0}{6h+h^{2} \over {h}}\\&=\lim _{h\to 0}(6+h)\\&=6\end{aligned}}}

La pendenza della retta tangente al quadratura funzione nel punto (3, 9) è di 6, che è a dire, è di andare fino a sei volte più veloce di come sta andando a destra. Il processo limite appena descritto può essere eseguito per qualsiasi punto nel dominio della funzione di quadratura. Questo definisce la funzione derivata della funzione di quadratura o solo la derivata della funzione di quadratura in breve. Un calcolo simile a quello sopra mostra che la derivata della funzione di quadratura è la funzione di raddoppio.
Notazione di Leibniz
Una notazione comune, introdotta da Leibniz, per la derivata nell’esempio precedente è
y = x 2 d y d x = 2 x . {\displaystyle {\begin{aligned}y&=x^{2}\\{\frac {dy}{dx}}&=2x.\end{aligned}}}

In un approccio basato sui limiti, il simbolo dy/dx deve essere interpretato non come il quoziente di due numeri ma come una scorciatoia per il limite calcolato sopra. Leibniz, tuttavia, intendeva rappresentare il quoziente di due numeri infinitesimalmente piccoli, dy essendo il cambiamento infinitesimalmente piccolo in y causato da un cambiamento infinitesimalmente piccolo dx applicato a x. Possiamo anche pensare a d / dx come un operatore di differenziazione, che prende una funzione come input e dà un’altra funzione, la derivata, come output. Ad esempio:
d d x ( x 2 ) = 2 x . {\displaystyle {\frac{d} {dx}}(x^{2})=2x.}

In questo utilizzo, il dx nel denominatore viene letto come “rispetto a x”. Un altro esempio di notazione corretta potrebbe essere:
g ( t ) = 2 t + 2 t + 4 d d t g ( t ) = 2 t + 2 {\displaystyle {\begin{aligned}g(t)=t^{2}+2t+4\\\\{d \dt}g(t)=2t+2\end{aligned}}}

Anche quando il calcolo è stato sviluppato utilizzando i limiti piuttosto che infinitesimi, è comune per manipolare simboli come dx e dy, come se fossero numeri reali; anche se è possibile evitare tali manipolazioni, a volte sono notationally conveniente esprimere operazioni come il totale derivati.
Calcolo integrale
Il calcolo integrale è lo studio delle definizioni, delle proprietà e delle applicazioni di due concetti correlati, l’integrale indefinito e l’integrale definito. Il processo di ricerca del valore di un integrale è chiamato integrazione. Nel linguaggio tecnico, il calcolo integrale studia due operatori lineari correlati.
L’integrale indefinito, noto anche come antiderivativo, è l’operazione inversa alla derivata. F è un integrale indefinito di f quando f è una derivata di F. (Questo uso di lettere minuscole e maiuscole per una funzione e il suo integrale indefinito è comune nel calcolo.)
L’integrale definito immette una funzione ed emette un numero, che dà la somma algebrica delle aree tra il grafico dell’input e l’asse X. La definizione tecnica dell’integrale definito comporta il limite di una somma di aree di rettangoli, chiamata somma di Riemann.
Un esempio motivante sono le distanze percorse in un dato momento.
D i s t a n c e = S p e e d ⋅ T i m e {\displaystyle \mathrm {Distance} =\mathrm {Speed} \cdot \mathrm {Tempo} }

Se la velocità è costante, solo la moltiplicazione è necessario, ma se la velocità cambia, il più potente metodo per trovare la distanza necessario. Uno di questi metodi consiste nell’approssimare la distanza percorsa suddividendo il tempo in molti brevi intervalli di tempo, quindi moltiplicando il tempo trascorso in ciascun intervallo per una delle velocità in quell’intervallo e quindi prendendo la somma (una somma di Riemann) della distanza approssimata percorsa in ciascun intervallo. L’idea di base è che se passa solo un breve periodo di tempo, la velocità rimarrà più o meno la stessa. Tuttavia, una somma di Riemann fornisce solo un’approssimazione della distanza percorsa. Dobbiamo prendere il limite di tutte queste somme di Riemann per trovare la distanza esatta percorsa.
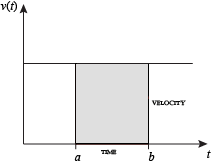

Quando la velocità è costante, la distanza totale percorsa nell’intervallo di tempo specificato può essere calcolata moltiplicando velocità e tempo. Ad esempio, viaggiando a 50 mph costanti per 3 ore si ottiene una distanza totale di 150 miglia. Nel diagramma a sinistra, quando la velocità costante e il tempo sono graficamente, questi due valori formano un rettangolo con altezza uguale alla velocità e larghezza uguale al tempo trascorso. Pertanto, il prodotto di velocità e tempo calcola anche l’area rettangolare sotto la curva di velocità (costante). Questa connessione tra l’area sotto una curva e la distanza percorsa può essere estesa a qualsiasi regione di forma irregolare che presenta una velocità fluttuante in un dato periodo di tempo. Se f(x) nel diagramma a destra rappresenta la velocità varia nel tempo, la distanza percorsa (tra le volte rappresentato da a e b) è l’area della regione ombreggiata s.
Per approssimare l’area, un metodo intuitivo sarebbe quello di dividere la distanza tra a e b in un numero di segmenti uguali, la lunghezza di ogni segmento rappresentato dal simbolo Δx. Per ogni piccolo segmento, possiamo scegliere un valore della funzione f (x). Chiama quel valore h. Quindi l’area del rettangolo con base Δx e altezza h dà la distanza (tempo Δx moltiplicato per velocità h) percorsa in quel segmento. Associato a ciascun segmento è il valore medio della funzione sopra di esso, f(x) = h. La somma di tutti questi rettangoli fornisce un’approssimazione dell’area tra l’asse e la curva, che è un’approssimazione della distanza totale percorsa. Un valore più piccolo per Δx darà più rettangoli e nella maggior parte dei casi un’approssimazione migliore, ma per una risposta esatta dobbiamo prendere un limite quando Δx si avvicina a zero.
Il simbolo dell’integrazione è ∫ {\displaystyle \int}

, una S allungata (la S sta per “somma”). L’integrale definito è scritto come: ∫ a b f (x ) d x . Per ulteriori informazioni, consultare il sito:}

e viene letto “l’integrale da a a b di f-of-x rispetto a x.” La notazione di Leibniz dx ha lo scopo di suggerire di dividere l’area sotto la curva in un numero infinito di rettangoli, in modo che la loro larghezza Δx diventi la dx infinitesimale piccola. In una formulazione del calcolo basata sui limiti, la notazione
∫ a b x d x {\displaystyle \int _{a}^{b}\cdots \,dx}

è da intendersi come un operatore che assume una funzione come input e dà un numero, l’area, come output. Il differenziale di terminazione, dx, non è un numero e non viene moltiplicato per f(x), sebbene, servendo come promemoria della definizione limite Δx, possa essere trattato come tale nelle manipolazioni simboliche dell’integrale. Formalmente, il differenziale indica la variabile su cui è integrata la funzione e funge da staffa di chiusura per l’operatore di integrazione.
L’integrale indefinito, o antiderivativo, è scritto:
∫ f ( x ) d x . {\stile di visualizzazione \ int f (x)\, dx.}

Le funzioni che differiscono solo da una costante hanno la stessa derivata, e si può dimostrare che l’antiderivativo di una data funzione è in realtà una famiglia di funzioni che differiscono solo da una costante. Poiché la derivata della funzione y = x2 + C, dove C è una costante qualsiasi, è y’ = 2x, l’antiderivativo di quest’ultimo è dato da:
∫ 2 x d x = x 2 + C . {\displaystyle \ int 2x\,dx=x^{2}+C.}

La costante C non specificata presente nell’integrale indefinito o antiderivativo è nota come costante di integrazione.
Teorema fondamentale
Il teorema fondamentale del calcolo afferma che la differenziazione e l’integrazione sono operazioni inverse. Più precisamente, mette in relazione i valori degli antiderivativi con integrali definiti. Poiché di solito è più facile calcolare un antiderivativo che applicare la definizione di un integrale definito, il teorema fondamentale del calcolo fornisce un modo pratico di calcolare integrali definiti. Può anche essere interpretato come una precisa affermazione del fatto che la differenziazione è l’inverso dell’integrazione.
Il teorema fondamentale degli stati di calcolo: Se una funzione f è continua sull’intervallo e se F è una funzione la cui derivata è f sull’intervallo (a, b), allora
∫ a b f ( x ) d x = F ( b ) − F ( a ) . Per maggiori informazioni clicca qui. il nostro sito utilizza cookie tecnici e di terze parti per migliorare la tua esperienza di navigazione.
Inoltre, per ogni x nell’intervallo (a, b),
d d x ∫ a x f ( t ) d t = f ( x ) . Per maggiori informazioni clicca qui. il nostro sito utilizza cookie tecnici e di terze parti.
Questa realizzazione, fatta sia da Newton che da Leibniz, che basarono i loro risultati su precedenti lavori di Isaac Barrow, fu la chiave per la proliferazione dei risultati analitici dopo che il loro lavoro divenne noto. Il teorema fondamentale fornisce un metodo algebrico di calcolo di molti integrali definiti-senza eseguire processi limite-trovando formule per antiderivativi. È anche una soluzione prototipo di un’equazione differenziale. Le equazioni differenziali riguardano una funzione sconosciuta ai suoi derivati e sono onnipresenti nelle scienze.