Récemment, je pensais à diverses justifications pour la définition de 0! (factorielle de zéro) qui est
$$0!=1
La valeur supposée de 1 peut sembler assez évidente si l’on considère la formule récursive. Cependant, cela ne m’a pas satisfait « mathématiquement ». C’est pourquoi j’ai décidé d’écrire ces quelques phrases. Je donnerai des motivations pour les moins avancés, mais il y aura aussi des motivations pour un peu plus d’initiés.
⭐️Factorielle dans la Calculatrice scalaire

⭐️ Factorielle et récurrence
Pour un entier n >0 factorielle est définie comme suit
$$n!= n\times(n-1) \times(n-2) \times\ldots\times 2\times 1
Avec facilité, vous pouvez voir que la formule récursive ci-dessous suit
nn!= n\ fois (n-1)!$$
11!=1⭐
⭐️0! = 1 – motivation basée sur la récurrence
Petite transformation de
$$n!= n\ fois (n-1)!$$
donne
$$(n-1)!= \frac {n!} {n}Subs
En remplaçant n = 1
$$(1-1)!= \frac {1!} {1}$$
00!=1!=1
Cette explication, bien que facile, ne fournit pas (à mon avis) une compréhension assez profonde de « pourquoi cela devrait être la meilleure option”.
⭐️ Factorielle n! compte les séquences distinctes possibles de n objets distincts (permutations)
Supposons que nous ayons un ensemble contenant n éléments
\\{1,2, \ldots, n \}Now
Maintenant, comptons l’ordre possible des éléments est cet ensemble
- n façons de sélectionner le premier élément (parce que nous avons l’ensemble entier disponible)
- n -1 façons de sélectionner le deuxième élément (parce que le premier a déjà été sélectionné, il y a n-1 gauche)
- n-2 façons de sélectionner le troisième élément (parce que les deux ont déjà été sélectionnés, il reste n-2)
- …
- n-(k-1) façons de sélectionner le numéro d’élément k (parce que les k-1 ont déjà été sélectionnés, n-(k-1) restent)
- 2 façons de sélectionner le numéro d’élément n-1 (parce que les n-2 ont été sélectionnés, il en reste encore 2)
- 1 façon de sélectionner le numéro d’élément n (parce que les n-1 ont été sélectionnés, il n’en reste qu’un)
Enfin, en comptant tous les moyens possibles, on obtient
$$n\times(n-1) \times(n-2) \times\ldots\times 2\ fois 1 = n!Conclusion
Conclusion : La factorielle de n compte le nombre de permutation d’un ensemble contenant n éléments.
⭐️ k-permutations de n parfois appelées permutations ou variations partielles
Les k-permutations de n sont les différents arrangements ordonnés d’un sous-ensemble d’éléments k d’un ensemble de n. Le nombre de telles k-permutations de n est
PP_k ^n = n\fois(n-1)\ fois(n-2)\ fois\ldots\fois \bigg(n-(k-1)\bigg) = \frac{n!} {(n-k)!} }
Il est facile de voir que n-permutation de n est une permutation, donc
$$P_n^n = n!$$
nn! = \frac {n!} {(n-n)!} = \frac {n!}{0!} }
Le prochain aperçu pourquoi 0!=1 est la définition correcte vient de celle pour tout n >0 nous devrions avoir
00! \ fois n! = n!⭐
⭐️ Fonctionne comme un mappage d’ensembles

Fonction
Functionf:A\to B$$
La fonction f: A → B, où pour tout a ∈ A il y a f(a) = b ∈ B, définit la relation entre les éléments a et b. On peut dire que les éléments a ∈ A et b ∈ B sont en relation « f” si et seulement si f(a) = b.
⭐️La fonction en tant que sous-ensemble de produit cartésien
La fonction est une relation binaire, ce qui signifie que la fonction peut être exprimée comme un sous-ensemble d’un produit cartésien.
⭐(a, b)\in f\subseteq A\times B\iff f(a)= b⭐
⭐️ Fonction injective

La fonction injective est une fonction qui préserve la distinction : elle ne mappe jamais des éléments distincts de son domaine au même élément de son codomain. Sous peu
⭐x\neq y\Rightarrow f(x) \neq f(y)$$
⭐️ Fonction surjective

Une fonction f est surjective (ou sur) si pour chaque élément b du codomain, il existe au moins un élément a dans le domaine tel que f(a) = b. Il n’est pas nécessaire que x soit unique.
$$f:A\à Bexist
{ {\large\displaystyle\forall_ {b\in B}\quad\displaystyle\exists_ {a\in A}\quad} f(a) = b⭐
⭐️ Fonction bijective

La fonction bijective, ou correspondance un à un, est une fonction où chaque élément d’un ensemble est apparié avec exactement un élément de l’autre ensemble, et chaque élément de l’autre ensemble est apparié avec exactement un élément du premier ensemble. Il n’y a pas d’éléments non appariés.
En termes mathématiques, une fonction bijective est à la fois un mappage injectif et surjectif d’un ensemble A à un ensemble B.
⭐️ Fonction bijective vs Permutation
La permutation est une fonction qui renvoie l’ordre d’un ensemble, c’est-à-dire que si nous considérons l’ensemble à n éléments {1, 2, n, n} alors la permutation sera une fonction
$$p: \{1, 2, n, n\}\ à \{1, 2 , n, n\}
satisfaisant la condition de fonction bijective.
En posant des questions sur le nombre de permutations, nous pouvons également poser des questions sur le nombre de bijections différentes d’un ensemble donné en lui-même.
⭐️ Fonction vide
Une fonction vide est toute fonction dont le domaine est un ensemble vide.
$$f:\emptyset\to B
La fonction vide « graphique” est un ensemble vide, car le produit cartésien du domaine et du codomain est vide.
$$\emptyset\times B = \emptyset
La fonction vide conserve la distinction (est injective), car dans le domaine (un ensemble vide) il n’y a pas deux éléments différents pour lesquels la valeur de la fonction est égale.
⭐️Un cas particulier d’une fonction vide
Analysons la fonction qui mappe un ensemble vide sur vide
ff:\emptyset\to\emptyset$$
Une telle fonction est une bijection car il s’agit d’une fonction injective (comme indiqué ci-dessus) et il n’y a aucun élément dans le codomain (le codomain est un ensemble vide) qui ne soit pas en relation avec les éléments du domaine.
Veuillez noter qu’il existe exactement une telle bijection, qui résulte du fait que la fonction est un sous-ensemble du produit cartésien du domaine et du codomain. Dans ce cas, ce n’est qu’un seul ensemble possible.
$$f:\emptyset\to\emptyset
$$\emptyset\times\emptyset=\emptysetThe
L’ensemble vide a exactement un sous-ensemble, qui est l’ensemble vide – une telle bijection est donc définie de manière unique.
⭐️ 0! = 1 vs Fonction vide
J’ai écrit ci-dessus que le nombre de permutations d’un ensemble de n éléments est égal au nombre de fonctions bijectives distinctes de cet ensemble dans lui-même.
Suivant – la permutation de l’ensemble de 0 éléments correspond à la bijection d’un ensemble vide dans l’ensemble vide /
Le cas particulier de la fonction vide est juste 1 – et j’ai présenté la preuve qu’il n’existe qu’une seule fonction de ce type 🙂
Un aperçu assez profond pourquoi 0! devrait par 1.
⭐️La fonction gamma
En mathématiques, la fonction Gamma est l’une des extensions de la fonction factorielle avec son argument décalé de 1, aux nombres réels et complexes.
$$\Gamma(z) = \displaystyle\int_0^{+\infty} t^{z-1} e^{-t}dt
Après intégration par parties, nous obtenons la formule récursive
formula\Gamma(z +1) =z\cdot\Gamma(z) see
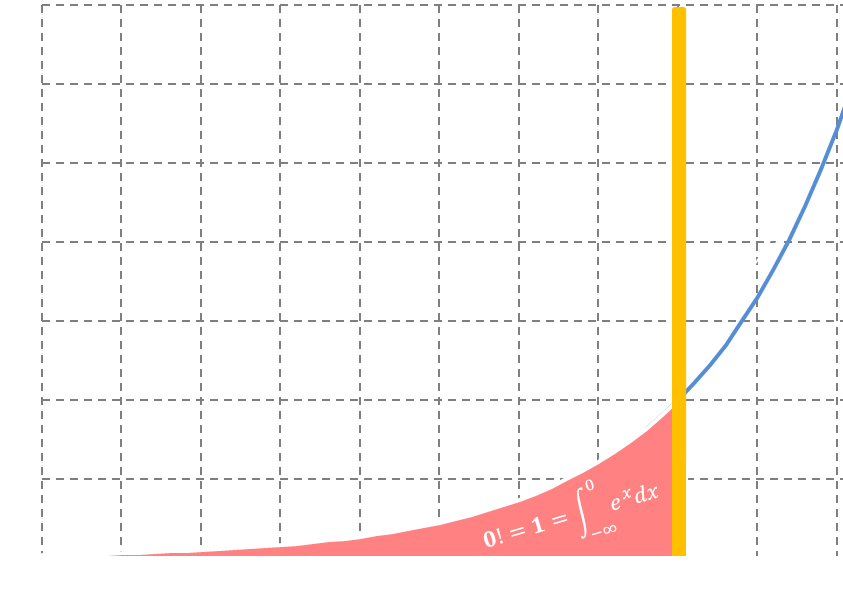
Voyons la valeur de
\\Gamma(1) =?$$
\\Gamma(1)=\displaystyle\int_0^{+\infty} e^{-t}dt=\displaystyle\int_{-\infty}^{0}e^{t}dtFollowing
Suivant
$$\Gamma(n+1) =n!$$
00! = \Gamma(1) = 1$$
⭐️ Scalar support for the Gamma function

Functions in Scalar Calculator, that support Gamma special function
- Gamma(x) – Gamma special function Γ(s)
- sgnGamma(x) – Signum of Gamma special function, Γ(s)
- logGamma(x) – Log Gamma special function, lnΓ(s)
- diGamma(x) – Digamma function as the logarithmic derivative of the Gamma special function, ψ(x)
- GammaL(s,x) – Lower incomplete gamma special function, γ(s,x)
- GammaU(s,x) – Upper incomplete Gamma special function, Γ(s,x)
- GammaP(s,x) , GammaRegL(s,x) – Lower regularized P gamma special function, P(s,x)
- GammaQ(s,x), GammaRegU(s,x) – Upper regularized Q Gamma special function, Q(s,x)
Gamma function chart

Gamma function vs Factorial chart

⭐️ Nombre e et relation factorielle
Basé sur l’expansion de la série de Taylor de e ^x, il est facile de montrer que
$$e =\displaystyle\sum_{n = 0}^\infty\frac{1}{n!} = \frac {1} {0!} +\frac {1} {1!}+\frac {1}{2!}+\frac {1}{3!}+\ldots$$
Sequence convergence

This is fascinating, as it shows even stronger relation of factorial to e
Thanks for reading! All the best 🙂