Limites et infinitésimaux
Le calcul est généralement développé en travaillant avec de très petites quantités. Historiquement, la première méthode de le faire était par des infinitésimaux. Ce sont des objets qui peuvent être traités comme des nombres réels mais qui sont, en quelque sorte, « infiniment petits ». Par exemple, un nombre infinitésimal peut être supérieur à 0, mais inférieur à n’importe quel nombre de la séquence 1, 1/2, 1/3,… et donc moins que tout nombre réel positif. De ce point de vue, le calcul est un ensemble de techniques de manipulation des infinitésimaux. Les symboles d x {\displaystyle dx}

et d y {\displaystyle dy}

ont été considérés comme infinitésimaux, et la dérivée d y/d x {\displaystyle dy/dx}

était simplement leur rapport.
L’approche infinitésimale est tombée en disgrâce au 19ème siècle car il était difficile de rendre précise la notion d’infinitésimale. Cependant, le concept a été relancé au 20ème siècle avec l’introduction d’une analyse non standard et d’une analyse infinitésimale fluide, qui ont fourni des bases solides pour la manipulation des infinitésimaux.
À la fin du 19e siècle, les infinitésimaux ont été remplacés dans le monde universitaire par l’approche epsilon, delta des limites. Les limites décrivent la valeur d’une fonction à une certaine entrée en fonction de ses valeurs aux entrées voisines. Ils capturent le comportement à petite échelle dans le contexte du système de nombres réels. Dans ce traitement, le calcul est un ensemble de techniques pour manipuler certaines limites. Les infinitésimaux sont remplacés par de très petits nombres, et le comportement infiniment petit de la fonction est trouvé en prenant le comportement limitant pour des nombres de plus en plus petits. On pensait que les limites fournissaient une base plus rigoureuse pour le calcul, et pour cette raison, elles sont devenues l’approche standard au cours du XXe siècle.
Calcul différentiel

Le calcul différentiel est l’étude de la définition, des propriétés et des applications de la dérivée d’une fonction. Le processus de recherche de la dérivée est appelé différenciation. Étant donné une fonction et un point du domaine, la dérivée en ce point est un moyen de coder le comportement à petite échelle de la fonction près de ce point. En trouvant la dérivée d’une fonction en chaque point de son domaine, il est possible de produire une nouvelle fonction, appelée la fonction dérivée ou simplement la dérivée de la fonction d’origine. En termes formels, la dérivée est un opérateur linéaire qui prend une fonction en entrée et produit une deuxième fonction en sortie. C’est plus abstrait que la plupart des processus étudiés en algèbre élémentaire, où les fonctions entrent généralement un nombre et en sortent un autre. Par exemple, si la fonction de doublement reçoit l’entrée trois, elle en sort six, et si la fonction de quadrature reçoit l’entrée trois, elle en sort neuf. La dérivée, cependant, peut prendre la fonction de quadrature comme entrée. Cela signifie que la dérivée prend toutes les informations de la fonction de quadrature — comme que deux est envoyé à quatre, trois est envoyé à neuf, quatre est envoyé à seize, et ainsi de suite — et utilise ces informations pour produire une autre fonction. La fonction produite en dérivant la fonction de quadrature s’avère être la fonction de doublement.
En termes plus explicites, la « fonction de doublement » peut être notée par g(x) =2x et la « fonction de quadrature » par f(x) = x2. La « dérivée » prend maintenant la fonction f(x), définie par l’expression « x2 », comme entrée, c’est—à—dire toutes les informations – telles que deux sont envoyées à quatre, trois sont envoyées à neuf, quatre sont envoyées à seize, et ainsi de suite – et utilise ces informations pour sortir une autre fonction, la fonction g(x) = 2x, comme il s’avérera.
Le symbole le plus courant pour une dérivée est une marque de type apostrophe appelée prime. Ainsi, la dérivée d’une fonction appelée f est notée f’, prononcée » f premier « . Par exemple, si f(x) = x2 est la fonction de quadrature, alors f'(x) = 2x est sa dérivée (la fonction de doublement g d’en haut). Cette notation est connue sous le nom de notation de Lagrange.
Si l’entrée de la fonction représente le temps, alors la dérivée représente le changement par rapport au temps. Par exemple, si f est une fonction qui prend un temps en entrée et donne la position d’une balle à ce moment-là en sortie, alors la dérivée de f est la façon dont la position change dans le temps, c’est-à-dire la vitesse de la balle.
Si une fonction est linéaire (c’est-à-dire si le graphe de la fonction est une droite), alors la fonction peut être écrite comme y = mx +b, où x est la variable indépendante, y est la variable dépendante, b est l’ordonnée à l’origine, et :
m = course de montée = changement de y changement de x = Δ y Δ x. {\displaystyle m = {\frac{\text{rise}}{\text{run}}} = {\frac {{\text{change in}}y}{{\text{change in}}x}} = {\frac{\Delta y}{\Delta x}}.}

Cela donne une valeur exacte pour la pente d’une ligne droite. Si le graphique de la fonction n’est pas une ligne droite, cependant, le changement de y divisé par le changement de x varie. Les dérivés donnent un sens exact à la notion de changement de sortie par rapport à la variation de l’entrée. Pour être concret, soit f une fonction, et fixer un point a dans le domaine de f. (a, f(a)) est un point sur le graphe de la fonction. Si h est un nombre proche de zéro, alors a + h est un nombre proche de a. Par conséquent, (a + h, f(a + h)) est proche de (a, f(a)). La pente entre ces deux points est
m = f(a+ h) − f(a)(a+h) − a = f(a+h) – f(a)h. {\displaystyle m = {\frac{f(a+h)-f(a)} {(a+h)-a}} = {\frac{f(a+h)-f(a)}{h}}.}

Cette expression est appelée quotient de différence. Une droite passant par deux points d’une courbe s’appelle une droite sécante, donc m est la pente de la droite sécante entre (a, f(a)) et (a + h, f(a +h)). La ligne sécante n’est qu’une approximation du comportement de la fonction au point a car elle ne tient pas compte de ce qui se passe entre a et a + h. Il n’est pas possible de découvrir le comportement en a en mettant h à zéro car cela nécessiterait une division par zéro, ce qui n’est pas défini. La dérivée est définie en prenant la limite car h tend vers zéro, ce qui signifie qu’elle considère le comportement de f pour toutes les petites valeurs de h et extrait une valeur cohérente pour le cas où h est égal à zéro :
lim h → 0 f(a + h) – f(a) h. {\displaystyle\lim_ {h\ à 0} {f(a+h) – f(a)\ sur {h}}.}

Géométriquement, la dérivée est la pente de la droite tangente au graphe de f en a. La droite tangente est une limite de droites sécantes tout comme la dérivée est une limite de quotients de différence. Pour cette raison, la dérivée est parfois appelée la pente de la fonction f.
Voici un exemple particulier, la dérivée de la fonction de quadrature à l’entrée 3. Soit f(x) = x2 la fonction de quadrature.

f ′ ( 3 ) = lim h → 0 ( 3 + h ) 2 − 3 2 h = lim h → 0 9 + 6 h + h 2 − 9 h = lim h → 0 6 h + h 2 h = lim h → 0 ( 6 + h ) = 6 {\displaystyle {\begin{aligned}f'(3)&=\lim _{h\to 0}{(3+h)^{2}-3^{2} \over {h}}\\&=\lim _{h\to 0}{9+6h+h^{2}-9 \over {h}}\\&=\lim _{h\to 0}{6h+h^{2} \over {h}}\\&=\lim _{h\to 0}(6+h)\\&=6\end{aligned}}}

La pente de la droite tangente à la fonction de quadrature au point (3, 9) est 6, c’est-à-dire qu’il monte six fois plus vite qu’il va vers la droite. Le processus limite qui vient d’être décrit peut être effectué pour n’importe quel point du domaine de la fonction de quadrature. Ceci définit la fonction dérivée de la fonction de quadrature ou simplement la dérivée de la fonction de quadrature pour faire court. Un calcul similaire à celui ci-dessus montre que la dérivée de la fonction de quadrature est la fonction de doublement.
Notation de Leibniz
Une notation courante, introduite par Leibniz, pour la dérivée dans l’exemple ci-dessus est
y = x 2 d y d x = 2 x. {\displaystyle {\begin{aligned} y &=x ^{2}\\{\frac{dy}{dx}} &=2x.\end{aligned}}}

Dans une approche basée sur des limites, le symbole dy/dx doit être interprété non pas comme le quotient de deux nombres mais comme un raccourci pour la limite calculée ci-dessus. Leibniz, cependant, avait l’intention de représenter le quotient de deux nombres infinitésimalement petits, dy étant le changement infinitésimalement petit de y causé par un changement infinitésimalement petit dx appliqué à x. Nous pouvons également penser à d / dx comme un opérateur de différenciation, qui prend une fonction en entrée et donne une autre fonction, la dérivée, en sortie. Par exemple :
d d x(x 2) = 2 x. {\displaystyle {\frac{d}{dx}}(x^{2}) = 2x. }

Dans cet usage, le dx du dénominateur est lu comme « par rapport à x ». Un autre exemple de notation correcte pourrait être:
g(t) = t 2 + 2 t + 4 d d t g (t) = 2 t + 2 {\displaystyle {\begin{aligné} g(t) = t^{2} + 2t + 4 \\\\ {d\ over dt} g(t) = 2t + 2\end {aligné}}}

Même lorsque le calcul est développé en utilisant des limites plutôt que des infinitésimaux, il est courant de manipuler des symboles comme dx et dy comme s’il s’agissait de nombres réels; bien qu’il soit possible d’éviter de telles manipulations, ils sont parfois pratiques notationnellement pour exprimer des opérations telles que la dérivée totale.
Calcul intégral
Le calcul intégral est l’étude des définitions, des propriétés et des applications de deux concepts connexes, l’intégrale indéfinie et l’intégrale définie. Le processus de recherche de la valeur d’une intégrale s’appelle l’intégration. En langage technique, le calcul intégral étudie deux opérateurs linéaires connexes.
L’intégrale indéfinie, également appelée antidérivative, est l’opération inverse de la dérivée. F est une intégrale indéfinie de f lorsque f est une dérivée de F. (Cette utilisation de lettres minuscules et majuscules pour une fonction et son intégrale indéfinie est courante en calcul.)
L’intégrale définie entre une fonction et produit un nombre, ce qui donne la somme algébrique des aires entre le graphe de l’entrée et l’axe des abscisses. La définition technique de l’intégrale définie implique la limite d’une somme d’aires de rectangles, appelée somme de Riemann.
Un exemple motivant est les distances parcourues dans un temps donné.
D i s t a n c e = S p e e d { T i m e {\displaystyle\mathrm {Distance} = \mathrm {Speed}\cdot\mathrm {Time}}

Si la vitesse est constante, seule la multiplication est nécessaire, mais si la vitesse change, une méthode plus puissante pour trouver la distance est nécessaire. Une telle méthode consiste à approximer la distance parcourue en divisant le temps en de nombreux intervalles de temps courts, puis en multipliant le temps écoulé dans chaque intervalle par l’une des vitesses de cet intervalle, puis en prenant la somme (une somme de Riemann) de la distance approximative parcourue dans chaque intervalle. L’idée de base est que si seulement un court laps de temps s’écoule, la vitesse restera plus ou moins la même. Cependant, une somme de Riemann ne donne qu’une approximation de la distance parcourue. Nous devons prendre la limite de toutes ces sommes de Riemann pour trouver la distance exacte parcourue.
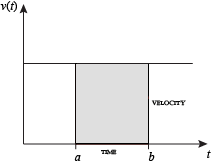
Lorsque la vitesse est constante, la distance totale parcourue sur l’intervalle de temps donné peut être calculée en multipliant la vitesse et le temps. Par exemple, parcourir une vitesse constante de 50 mi / h pendant 3 heures se traduit par une distance totale de 150 miles. Dans le diagramme de gauche, lorsque la vitesse et le temps constants sont représentés, ces deux valeurs forment un rectangle de hauteur égale à la vitesse et de largeur égale au temps écoulé. Par conséquent, le produit de la vitesse et du temps calcule également la surface rectangulaire sous la courbe de vitesse (constante). Cette liaison entre l’aire sous une courbe et la distance parcourue peut être étendue à toute région de forme irrégulière présentant une vitesse fluctuante sur une période de temps donnée. Si f(x) dans le diagramme de droite représente la vitesse telle qu’elle varie dans le temps, la distance parcourue (entre les temps représentés par a et b) est l’aire de la région ombragée s.
Pour approximer cette aire, une méthode intuitive consisterait à diviser la distance entre a et b en un nombre de segments égaux, la longueur de chaque segment étant représentée par le symbole Δx. Pour chaque petit segment, nous pouvons choisir une valeur de la fonction f(x). Appelez cette valeur h. Alors l’aire du rectangle avec la base Δx et la hauteur h donne la distance (temps Δx multiplié par la vitesse h) parcourue dans ce segment. La valeur moyenne de la fonction au-dessus de chaque segment est associée à f (x) = h. La somme de tous ces rectangles donne une approximation de l’aire entre l’axe et la courbe, qui est une approximation de la distance totale parcourue. Une valeur plus petite pour Δx donnera plus de rectangles et dans la plupart des cas une meilleure approximation, mais pour une réponse exacte, nous devons prendre une limite lorsque Δx approche de zéro.
Le symbole de l’intégration est {{\displaystyle\int}

, un S allongé (le S signifie « somme »). L’intégrale définie s’écrit comme: a a b f(x) d x. {\displaystyle\int_{a}^{b} f(x)\, dx.}

et se lit « l’intégrale de a à b de f-de-x par rapport à x ». La notation de Leibniz dx est destinée à suggérer de diviser l’aire sous la courbe en un nombre infini de rectangles, de sorte que leur largeur Δx devienne l’infinitésimalement petite dx. Dans une formulation du calcul basée sur des limites, la notation
∫ a b ⋯d x {\displaystyle\int_{a}^{b}\cdots\, dx}

doit être comprise comme un opérateur qui prend une fonction comme entrée et donne un nombre, l’aire, comme sortie. La différentielle de terminaison, dx, n’est pas un nombre, et n’est pas multipliée par f(x), bien que, rappelant la définition de limite Δx, elle puisse être traitée comme telle dans des manipulations symboliques de l’intégrale. Formellement, le différentiel indique la variable sur laquelle la fonction est intégrée et sert de parenthèse de fermeture pour l’opérateur d’intégration.
L’intégrale indéfinie, ou antidérivative, s’écrit :
∫ f(x)d x. {\displaystyle\int f(x)\, dx.}

Les fonctions ne différant que par une constante ont la même dérivée, et on peut montrer que l’antidérivative d’une fonction donnée est en fait une famille de fonctions ne différant que par une constante. Puisque la dérivée de la fonction y = x2 +C, où C est une constante quelconque, est y’ = 2x, l’antidérivative de cette dernière est donnée par :
∫ 2 x d x = x 2 +C. {\displaystyle\int 2x\, dx = x^{2} +C. }

La constante non spécifiée C présente dans l’intégrale indéfinie ou l’antidérivative est connue comme la constante d’intégration.
Théorème fondamental
Le théorème fondamental du calcul stipule que la différenciation et l’intégration sont des opérations inverses. Plus précisément, il relie les valeurs des antidérivatifs aux intégrales définies. Parce qu’il est généralement plus facile de calculer une antidérivative que d’appliquer la définition d’une intégrale définie, le théorème fondamental du calcul fournit un moyen pratique de calculer des intégrales définies. Il peut également être interprété comme une déclaration précise du fait que la différenciation est l’inverse de l’intégration.
Le théorème fondamental des états de calcul: Si une fonction f est continue sur l’intervalle et si F est une fonction dont la dérivée est f sur l’intervalle (a, b), alors
∫ a b f(x) d x = F(b) – F(a). {\displaystyle\int_{a}^{b} f(x)\, dx = F(b) – F(a).}

De plus, pour chaque x de l’intervalle (a, b),
d d x ∫ a x f(t) d t = f(x). {\displaystyle{\frac{d}{dx}}\int_{a}^{x} f(t)\, dt = f(x).}

Cette réalisation, faite par Newton et Leibniz, qui ont basé leurs résultats sur des travaux antérieurs d’Isaac Barrow, a été la clé de la prolifération des résultats analytiques après que leurs travaux ont été connus. Le théorème fondamental fournit une méthode algébrique de calcul de nombreuses intégrales définies — sans effectuer de processus limites – en trouvant des formules pour les antidérivatives. C’est aussi une solution prototype d’une équation différentielle. Les équations différentielles relient une fonction inconnue à ses dérivées, et sont omniprésentes dans les sciences.