Límites e infinitesimales
El cálculo se desarrolla generalmente trabajando con cantidades muy pequeñas. Históricamente, el primer método para hacerlo fue por infinitesimales. Estos son objetos que se pueden tratar como números reales, pero que son, en cierto sentido, «infinitamente pequeños». Por ejemplo, un número infinitesimal podría ser mayor que 0, pero menor que cualquier número en la secuencia 1, 1/2, 1/3, … y por lo tanto menos que cualquier número real positivo. Desde este punto de vista, el cálculo es una colección de técnicas para manipular infinitesimales. Los símbolos d x {\displaystyle dx}

y d y {\displaystyle dy}

fueron tomadas para ser infinitesimal, y el derivado de d y / d x {\displaystyle dy/dx}

era simplemente su relación.
El enfoque infinitesimal cayó en desgracia en el siglo XIX porque era difícil hacer precisa la noción de un infinitesimal. Sin embargo, el concepto fue revivido en el siglo XX con la introducción del análisis no estándar y el análisis infinitesimal suave, que proporcionó bases sólidas para la manipulación de infinitesimales.
A finales del siglo XIX, los infinitesimales fueron reemplazados dentro de la academia por el epsilon, enfoque delta de los límites. Los límites describen el valor de una función en una entrada determinada en términos de sus valores en entradas cercanas. Capturan el comportamiento a pequeña escala en el contexto del sistema de números reales. En este tratamiento, el cálculo es una colección de técnicas para manipular ciertos límites. Los infinitesimales son reemplazados por números muy pequeños, y el comportamiento infinitamente pequeño de la función se encuentra tomando el comportamiento limitante para números cada vez más pequeños. Se pensó que los límites proporcionaban una base más rigurosa para el cálculo, y por esta razón se convirtieron en el enfoque estándar durante el siglo XX.
cálculo Diferencial

el cálculo Diferencial es el estudio de la definición, propiedades y aplicaciones de la derivada de una función. El proceso de encontrar la derivada se llama diferenciación. Dada una función y un punto en el dominio, la derivada en ese punto es una forma de codificar el comportamiento a pequeña escala de la función cerca de ese punto. Al encontrar la derivada de una función en cada punto de su dominio, es posible producir una nueva función, llamada la función derivada o simplemente la derivada de la función original. En términos formales, la derivada es un operador lineal que toma una función como entrada y produce una segunda función como salida. Esto es más abstracto que muchos de los procesos estudiados en álgebra elemental, donde las funciones generalmente ingresan un número y generan otro número. Por ejemplo, si a la función de duplicación se le da la entrada tres, entonces produce seis, y si a la función de cuadratura se le da la entrada tres, entonces produce nueve. La derivada, sin embargo, puede tomar la función de cuadratura como entrada. Esto significa que la derivada toma toda la información de la función de cuadratura, como que dos se envía a cuatro, tres se envía a nueve, cuatro se envía a dieciséis, y así sucesivamente, y usa esta información para producir otra función. La función producida por derivar la función de cuadratura resulta ser la función de duplicación.
En términos más explícitos, la » función de duplicación «puede ser denotada por g(x) = 2x y la» función de cuadratura » por f(x) = x2. La «derivada» ahora toma la función f(x), definida por la expresión «x2», como una entrada, que es toda la información, como que dos se envía a cuatro, tres se envía a nueve, cuatro se envía a dieciséis, y así sucesivamente, y usa esta información para generar otra función, la función g (x) = 2x, como resultará.
El símbolo más común para una derivada es una marca tipo apóstrofo llamada primo. Por lo tanto, la derivada de una función llamada f se denota por f’, que se pronuncia «f primo». Por ejemplo, si f ( x) = x2 es la función de cuadratura, entonces f'(x) = 2x es su derivada (la función de duplicación g desde arriba). Esta notación se conoce como notación de Lagrange.
Si la entrada de la función representa el tiempo, entonces la derivada representa el cambio con respecto al tiempo. Por ejemplo, si f es una función que toma un tiempo como entrada y da la posición de una bola en ese momento como salida, entonces la derivada de f es cómo la posición está cambiando en el tiempo, es decir, es la velocidad de la bola.
Si una función es lineal (es decir, si el gráfico de la función es una línea recta), entonces la función se puede escribir como y = mx + b, donde x es la variable independiente, y es la variable dependiente, b es la intersección en y, y:
m = carrera de subida = cambio en y cambio en x = Δ y Δ x . {\displaystyle m={\frac {\text{lugar}}{\text{ejecutar}}}={\frac {{\text{cambio }}y}{{\text{cambio }}x}}={\frac {\Delta y}{\Delta x}}.}

Esto da un valor exacto para la pendiente de una línea recta. Sin embargo, si el gráfico de la función no es una línea recta, entonces el cambio en y dividido por el cambio en x varía. Los derivados dan un significado exacto a la noción de cambio en la producción con respecto al cambio en la entrada. Para ser concreto, sea f una función, y fije un punto a en el dominio de f. (a, f (a)) es un punto en el gráfico de la función. Si h es un número cercano a cero, entonces a + h es un número cercano a una. Por lo tanto, (a + h, f(a + h)) es cercano a (a, f(a)). La pendiente entre estos dos puntos es
m = f ( a + h ) − f ( a ) ( a + h ) − a = f ( a + h ) − f ( a ) h . {\displaystyle m={\frac {f(a+h)-f(a)}{(a+h)-a}}={\frac {f(a+h)-f(a)}{h}}.}

Esta expresión se denomina cociente de la diferencia. Una recta que pasa por dos puntos de una curva se denomina línea secante, por lo que m es la pendiente de la recta secante entre (a, f(a)) y (a + h, f(a + h)). La línea secante es solo una aproximación al comportamiento de la función en el punto a porque no tiene en cuenta lo que sucede entre a y a + h. No es posible descubrir el comportamiento en a estableciendo h a cero porque esto requeriría dividir por cero, que es indefinido. La derivada se define tomando el límite como h tiende a cero, lo que significa que considera el comportamiento de f para todos los valores pequeños de h y extrae un valor consistente para el caso en que h es igual a cero:
lim h → 0 f ( a + h ) − f ( a ) h . {\displaystyle \lim _ {h\to 0}{f (a + h) – f(a) \over {h}}.}

Geométricamente, la derivada es la pendiente de la recta tangente a la gráfica de f en a. La recta tangente es un límite de líneas secantes al igual que la derivada es un límite de cocientes de diferencia. Por esta razón, la derivada a veces se llama la pendiente de la función f.
Aquí hay un ejemplo particular, la derivada de la función de cuadratura en la entrada 3. Sea f (x) = x2 la función de cuadratura.

f ′ ( 3 ) = lim h → 0 ( 3 + h ) 2 − 3 2 h = lim h → 0 9 + 6 h + h 2 − 9 h = lim h → 0 6 h + h 2 h = lim h → 0 ( 6 + h ) = 6 {\displaystyle {\begin{aligned}f'(3)&=\lim _{h\to 0}{(3+h)^{2}-3^{2} \over {h}}\\&=\lim _{h\to 0}{9+6h+h^{2}-9 \over {h}}\\&=\lim _{h\to 0}{6h+h^{2} \over {h}}\\&=\lim _{h\to 0}(6+h)\\&=6\end{aligned}}}

La pendiente de la línea tangente a la cuadratura de la función en el punto (3, 9) es de 6, es decir, se va hasta seis veces más rápido de lo que se va a la derecha. El proceso límite que acabamos de describir se puede realizar para cualquier punto del dominio de la función de cuadratura. Esto define la función derivada de la función de cuadratura o simplemente la derivada de la función de cuadratura para abreviar. Un cálculo similar al anterior muestra que la derivada de la función de cuadratura es la función de duplicación.
Notación de Leibniz
Una notación común, introducida por Leibniz, para la derivada en el ejemplo anterior es
y = x 2 d y d x = 2 x . {\displaystyle {\begin{aligned}y&=x^{2}\\{\frac {dy}{dx}}&=2x.\end{aligned}}}

En un enfoque basado en límites, el símbolo dy/dx debe interpretarse no como el cociente de dos números, sino como una abreviatura para el límite calculado anteriormente. Leibniz, sin embargo, pretendía representar el cociente de dos números infinitesimalmente pequeños, dy es el cambio infinitesimalmente pequeño en y causado por un cambio infinitesimalmente pequeño dx aplicado a x. También podemos pensar en d/dx como un operador de diferenciación, que toma una función como entrada y da otra función, la derivada, como salida. Por ejemplo:
d d x (x 2) = 2 x . {\displaystyle {\frac {d}{dx}}(x^{2})=2x.}

En este uso, el dx en el denominador se lee como «con respecto a x». Otro ejemplo de notación correcta podría ser:
g ( t ) = t 2 + 2 t + 4 d d t g ( t ) = 2 t + 2 {\displaystyle {\begin{aligned}g(t)=t^{2}+2t+4\\\\{d \over dt}g(t)=2t+2\end{aligned}}}

Incluso cuando el cálculo se desarrolla utilizando límites en lugar de infinitesimales, es común manipular símbolos como dx y dy como si fueran números reales; aunque es posible evitar tales manipulaciones, a veces son notacionalmente convenientes para expresar operaciones como la derivada total.
Cálculo integral
El cálculo integral es el estudio de las definiciones, propiedades y aplicaciones de dos conceptos relacionados, la integral indefinida y la integral definida. El proceso de encontrar el valor de una integral se llama integración. En lenguaje técnico, el cálculo integral estudia dos operadores lineales relacionados.
La integral indefinida, también conocida como la primitiva, es la operación inversa a la derivada. F es una integral indefinida de f cuando f es una derivada de F. (Este uso de letras mayúsculas y minúsculas para una función y su integral indefinida es común en cálculo.)
La integral definida ingresa una función y genera un número, que da la suma algebraica de áreas entre el gráfico de la entrada y el eje x. La definición técnica de la integral definida implica el límite de una suma de áreas de rectángulos, llamada suma de Riemann.
Un ejemplo motivador son las distancias recorridas en un tiempo determinado.
D i s t a n c e = S p e e d ⋅ T i m e {\displaystyle \mathrm {Distancia} =\mathrm {Velocidad} \cdot \mathrm {Tiempo} }

Si la velocidad es constante, solo se necesita multiplicación, pero si la velocidad cambios de velocidad, es necesario un método más potente para encontrar la distancia. Uno de estos métodos es aproximar la distancia recorrida dividiendo el tiempo en muchos intervalos cortos de tiempo, luego multiplicando el tiempo transcurrido en cada intervalo por una de las velocidades en ese intervalo, y luego tomando la suma (una suma de Riemann) de la distancia aproximada recorrida en cada intervalo. La idea básica es que si solo transcurre un corto tiempo, la velocidad se mantendrá más o menos igual. Sin embargo, una suma de Riemann solo da una aproximación de la distancia recorrida. Debemos tomar el límite de todas esas sumas de Riemann para encontrar la distancia exacta recorrida.
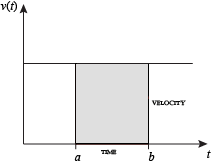

Cuando la velocidad es constante, la distancia total recorrida durante el intervalo de tiempo dado se puede calcular multiplicando la velocidad y el tiempo. Por ejemplo, viajar a 50 millas por hora durante 3 horas resulta en una distancia total de 150 millas. En el diagrama de la izquierda, cuando se representan la velocidad y el tiempo constantes, estos dos valores forman un rectángulo con altura igual a la velocidad y anchura igual al tiempo transcurrido. Por lo tanto, el producto de velocidad y tiempo también calcula el área rectangular bajo la curva de velocidad (constante). Esta conexión entre el área bajo una curva y la distancia recorrida se puede extender a cualquier región de forma irregular que exhiba una velocidad fluctuante durante un período de tiempo dado. Si f(x) en el diagrama de la derecha representa la velocidad a medida que varía con el tiempo, la distancia recorrida (entre los tiempos representados por a y b) es el área de la región sombreada s.
Para aproximar esa área, un método intuitivo sería dividir la distancia entre a y b en un número de segmentos iguales, la longitud de cada segmento representada por el símbolo Δx. Para cada segmento pequeño, podemos elegir un valor de la función f (x). Llame a ese valor h. Luego, el área del rectángulo con base Δx y altura h da la distancia (tiempo Δx multiplicado por velocidad h) recorrida en ese segmento. Asociado a cada segmento está el valor promedio de la función por encima de él, f(x) = h. La suma de todos estos rectángulos da una aproximación del área entre el eje y la curva, que es una aproximación de la distancia total recorrida. Un valor más pequeño para Δx dará más rectángulos y en la mayoría de los casos una mejor aproximación, pero para una respuesta exacta necesitamos tomar un límite cuando Δx se acerca a cero.
El símbolo de integración es ∫ {\displaystyle \ int }

, una S alargada (la S significa «suma»). La integral definida se escribe como: ∫ a b f (x ) d x . {\displaystyle \ int _ {a}^{b}f (x)\, dx.}

y se lee «la integral de a a b de f-de-x con respecto a x». La notación de Leibniz dx pretende sugerir dividir el área bajo la curva en un número infinito de rectángulos, de modo que su ancho Δx se convierta en el dx infinitesimalmente pequeño. En una formulación del cálculo basada en límites, la notación
∫ a b d d x {\displaystyle \int _{a}^{b}\cdots \,dx}

debe entenderse como un operador que toma una función como entrada y da un número, el área, como salida. El diferencial de terminación, dx, no es un número, y no se multiplica por f(x), aunque, sirviendo como recordatorio de la definición de límite Δx, puede tratarse como tal en manipulaciones simbólicas de la integral. Formalmente, el diferencial indica la variable sobre la que está integrada la función y sirve como soporte de cierre para el operador de integración.
La integral indefinida, o primitiva, se escribe:
∫ f (x ) d x . {\displaystyle \int f(x)\,dx.}

Las funciones que difieren solo por una constante tienen la misma derivada, y se puede demostrar que la primitiva de una función dada es en realidad una familia de funciones que difieren solo por una constante. Dado que la derivada de la función y = x2 + C, donde C es cualquier constante, es y ‘ = 2x, la primitiva de esta última viene dada por:
∫ 2 x d x = x 2 + C. {\displaystyle \int 2x\, dx = x^{2}+C.}

La constante C no especificada presente en la integral indefinida o antiderivada se conoce como la constante de integración.
teorema Fundamental
El teorema fundamental del cálculo establece que la diferenciación y la integración son operaciones inversas. Más precisamente, relaciona los valores de las antiderivadas con integrales definidas. Debido a que generalmente es más fácil calcular una primitiva que aplicar la definición de una integral definida, el teorema fundamental del cálculo proporciona una forma práctica de calcular integrales definidas. También puede interpretarse como una declaración precisa del hecho de que la diferenciación es lo contrario de la integración.
El teorema fundamental de los estados de cálculo: Si una función f es continua en el intervalo y si F es una función cuya derivada es f en el intervalo (a, b), entonces
∫ a b f ( x ) d x = F ( b ) − F ( a ) . {\displaystyle \ int _ {a}^{b} f (x)\, dx = F(b)-F (a).}

Además, para cada x en el intervalo (a, b),
d d x ∫ x f ( t ) d t = f ( x ) . {\displaystyle {\frac {d}{dx}} \ int _{a}^{x} f(t)\,dt=f (x).}

Esta realización, realizada por Newton y Leibniz, que basaron sus resultados en trabajos anteriores de Isaac Barrow, fue clave para la proliferación de resultados analíticos después de que su trabajo se conociera. El teorema fundamental proporciona un método algebraico para calcular muchas integrales definidas – sin realizar procesos límite-mediante la búsqueda de fórmulas para las antiderivadas. También es una solución prototipo de una ecuación diferencial. Las ecuaciones diferenciales relacionan una función desconocida con sus derivadas, y son ubicuas en las ciencias.