Grenzen und Infinitesimale
Kalkül wird normalerweise durch Arbeiten mit sehr kleinen Mengen entwickelt. Historisch gesehen war die erste Methode, dies zu tun, infinitesimal. Dies sind Objekte, die wie reelle Zahlen behandelt werden können, aber in gewissem Sinne „unendlich klein“ sind. Zum Beispiel könnte eine infinitesimale Zahl größer als 0 sein, aber kleiner als eine beliebige Zahl in der Sequenz 1, 1/2, 1/3, … und damit weniger als jede positive reelle Zahl. Unter diesem Gesichtspunkt ist die Infinitesimalrechnung eine Sammlung von Techniken zur Manipulation von Infinitesimalen. Die Symbole d x {\displaystyle dx}

und d y {\displaystyle dy}

wurden als infinitesimal angesehen, und die Ableitung d y/ d x {\displaystyle dy/dx}

war einfach ihr Verhältnis. Der infinitesimale Ansatz fiel im 19.Jahrhundert in Ungnade, weil es schwierig war, den Begriff eines Infinitesimalen zu präzisieren. Das Konzept wurde jedoch im 20.Jahrhundert mit der Einführung der nichtstandardisierten Analyse und der glatten Infinitesimalanalyse wiederbelebt, die solide Grundlagen für die Manipulation von Infinitesimalen lieferte.Im späten 19.Jahrhundert wurden Infinitesimale innerhalb der Wissenschaft durch den Epsilon-Delta-Ansatz für Grenzen ersetzt. Grenzwerte beschreiben den Wert einer Funktion an einem bestimmten Eingang in Bezug auf ihre Werte an nahe gelegenen Eingängen. Sie erfassen kleinräumiges Verhalten im Kontext des reellen Zahlensystems. In dieser Behandlung ist Kalkül eine Sammlung von Techniken zur Manipulation bestimmter Grenzen. Infinitesimale werden durch sehr kleine Zahlen ersetzt, und das unendlich kleine Verhalten der Funktion wird gefunden, indem das Begrenzungsverhalten für immer kleinere Zahlen verwendet wird. Es wurde angenommen, dass Grenzwerte eine strengere Grundlage für die Infinitesimalrechnung bilden, und aus diesem Grund wurden sie im zwanzigsten Jahrhundert zum Standardansatz.
Differentialrechnung

Differentialrechnung ist das Studium der Definition, Eigenschaften und Anwendungen der Ableitung einer Funktion. Der Prozess des Findens der Ableitung wird Differenzierung genannt. Bei einer gegebenen Funktion und einem Punkt in der Domäne ist die Ableitung an diesem Punkt eine Möglichkeit, das kleinräumige Verhalten der Funktion in der Nähe dieses Punktes zu codieren. Durch das Finden der Ableitung einer Funktion an jedem Punkt in ihrer Domäne ist es möglich, eine neue Funktion zu erzeugen, die als Ableitungsfunktion oder nur als Ableitung der ursprünglichen Funktion bezeichnet wird. Formal gesehen ist die Ableitung ein linearer Operator, der eine Funktion als Eingabe verwendet und eine zweite Funktion als Ausgabe erzeugt. Dies ist abstrakter als viele der in der elementaren Algebra untersuchten Prozesse, bei denen Funktionen normalerweise eine Zahl eingeben und eine andere Zahl ausgeben. Wenn beispielsweise die Verdoppelungsfunktion den Eingang drei erhält, gibt sie sechs aus, und wenn die Quadraturfunktion den Eingang drei erhält, gibt sie neun aus. Die Ableitung kann jedoch die Quadraturfunktion als Eingabe verwenden. Dies bedeutet, dass die Ableitung alle Informationen der Quadrierfunktion übernimmt — z. B. dass zwei an vier, drei an neun, vier an sechzehn usw. gesendet werden — und diese Informationen verwendet, um eine andere Funktion zu erzeugen. Die Funktion, die durch Ableiten der Quadrierfunktion erzeugt wird, stellt sich als Verdoppelungsfunktion heraus.Expliziter ausgedrückt kann die „Verdopplungsfunktion“ mit g(x) = 2x und die „Quadraturfunktion“ mit f(x) = x2 bezeichnet werden. Die „Ableitung“ nimmt nun die Funktion f (x), definiert durch den Ausdruck „x2“, als Eingabe, dh alle Informationen — z. B. dass zwei an vier, drei an neun, vier an sechzehn usw. gesendet werden — und verwendet diese Informationen, um eine andere Funktion auszugeben, die Funktion g (x) = 2x, wie sich herausstellen wird.
Das gebräuchlichste Symbol für eine Ableitung ist eine apostrophartige Markierung namens Primzahl. Somit wird die Ableitung einer Funktion namens f mit f‘ bezeichnet, ausgesprochen „f prime“. Wenn zum Beispiel f(x) = x2 die Quadraturfunktion ist, dann ist f'(x) = 2x ihre Ableitung (die Verdoppelungsfunktion g von oben). Diese Notation ist als Lagrange-Notation bekannt.
Wenn die Eingabe der Funktion die Zeit darstellt, repräsentiert die Ableitung die Änderung in Bezug auf die Zeit. Wenn zum Beispiel f eine Funktion ist, die eine Zeit als Eingabe verwendet und die Position eines Balls zu diesem Zeitpunkt als Ausgabe angibt, dann ist die Ableitung von f, wie sich die Position in der Zeit ändert, das heißt, es ist die Geschwindigkeit des Balls.
Wenn eine Funktion linear ist (dh wenn der Graph der Funktion eine gerade Linie ist), kann die Funktion als y = mx + b geschrieben werden, wobei x die unabhängige Variable ist, y die abhängige Variable ist, b der y-Schnittpunkt ist und:
m = rise run = Änderung von y Änderung von x = Δ y Δ x. {\displaystyle m={\frac {\text{Aufstieg}}{\text{Lauf}}}={\frac {{\text{Änderung in }}y}{{\text{Änderung in }}x}}={\frac {\Delta y}{\Delta x}}.}

Dies ergibt einen exakten Wert für die Steigung einer Geraden. Wenn der Graph der Funktion jedoch keine gerade Linie ist, variiert die Änderung in y geteilt durch die Änderung in x. Ableitungen geben dem Begriff der Änderung der Ausgabe in Bezug auf die Änderung der Eingabe eine genaue Bedeutung. Um konkret zu sein, sei f eine Funktion und fixiere einen Punkt a im Bereich von f. (a, f(a)) ist ein Punkt im Graphen der Funktion. Wenn h eine Zahl nahe Null ist, dann ist a + h eine Zahl nahe a. Daher ist (a + h, f(a + h)) nahe (a, f(a)). Die Steigung zwischen diesen beiden Punkten ist
m = f ( a + h ) − f ( a ) ( a + h ) − a = f ( a + h ) − f ( a ) h. {\displaystyle m={\frac {f(a+h)-f(a)}{(a+h)-a}}={\frac {f(a+h)-f(a)}{h}}.}

Dieser Ausdruck wird als Differenzquotient bezeichnet. Eine Linie durch zwei Punkte auf einer Kurve wird als Sekantenlinie bezeichnet, daher ist m die Steigung der Sekantenlinie zwischen (a, f (a)) und (a + h, f(a + h)). Die Sekantenlinie ist nur eine Annäherung an das Verhalten der Funktion am Punkt a, da sie nicht berücksichtigt, was zwischen a und a + h . Es ist nicht möglich, das Verhalten an a zu ermitteln, indem h auf Null gesetzt wird, da dies eine Division durch Null erfordern würde, was undefiniert ist. Dies bedeutet, dass das Verhalten von f für alle kleinen Werte von h berücksichtigt und ein konsistenter Wert für den Fall extrahiert wird, dass h gleich Null ist:
lim h → 0 f ( a + h ) − f ( a ) h. {\displaystyle \lim _{h\bis 0}{f(a+h)-f(a) \über {h}}.}

Geometrisch ist die Ableitung die Steigung der Tangentenlinie zum Graphen von f bei a. Die Tangentenlinie ist eine Grenze von Sekantenlinien, genau wie die Ableitung eine Grenze von Differenzquotienten ist. Aus diesem Grund wird die Ableitung manchmal als Steigung der Funktion f bezeichnet.
Hier ist ein besonderes Beispiel, die Ableitung der Quadraturfunktion am Eingang 3. Sei f (x) = x2 die Quadraturfunktion.

f ′ ( 3 ) = lim h → 0 ( 3 + h ) 2 − 3 2 h = lim h → 0 9 + 6 h + h 2 − 9 h = lim h → 0 6 h + h 2 h = lim h → 0 ( 6 + h ) = 6 {\displaystyle {\begin{aligned}f'(3)&=\lim _{h\to 0}{(3+h)^{2}-3^{2} \over {h}}\\&=\lim _{h\to 0}{9+6h+h^{2}-9 \over {h}}\\&=\lim _{h\to 0}{6h+h^{2} \over {h}}\\&=\lim _{h\to 0}(6+h)\\&=6\end{aligned}}}

Die Steigung der Tangente an die Quadraturfunktion am Punkt (3, 9) beträgt 6 das heißt, es geht sechsmal so schnell nach oben wie nach rechts. Der soeben beschriebene Grenzvorgang kann für jeden beliebigen Punkt im Bereich der Quadrierfunktion durchgeführt werden. Dies definiert die Ableitungsfunktion der Quadraturfunktion oder kurz nur die Ableitung der Quadraturfunktion. Eine Berechnung ähnlich der obigen zeigt, dass die Ableitung der Quadrierfunktion die Verdoppelungsfunktion ist.
Leibniz-Notation
Eine von Leibniz eingeführte allgemeine Notation für die Ableitung im obigen Beispiel ist
y = x 2 d y d x = 2 x. {\displaystyle {\begin{ausgerichtet}y&=x^{2}\\{\frac {dy}{dx}}&=2x.\end{ausgerichtet}}}

Bei einem grenzwertbasierten Ansatz ist das Symbol dy/dx nicht als Quotient zweier Zahlen zu interpretieren, sondern als Abkürzung für den oben berechneten Grenzwert. Leibniz beabsichtigte jedoch, den Quotienten zweier infinitesimal kleiner Zahlen darzustellen, wobei dy die infinitesimal kleine Änderung von y ist, die durch eine infinitesimal kleine Änderung verursacht wird dx angewendet auf x. Wir können uns d / dx auch als Differenzierungsoperator vorstellen, der eine Funktion als Eingabe verwendet und eine andere Funktion, die Ableitung, als Ausgabe angibt. Zum Beispiel:
d d x ( x 2 ) = 2 x. {\displaystyle {\frac {d}{dx}}(x^{2})=2x.}

Bei dieser Verwendung wird das dx im Nenner als „in Bezug auf x“ gelesen. Ein anderes Beispiel für korrekte Notation könnte sein:
g (t ) = t 2 + 2 t + 4 d d t g (t ) = 2 t + 2 {\displaystyle {\begin{ausgerichtet}g(t)=t^{2}+2t+4\\\\{d \über dt}g(t)=2t+2\end{ausgerichtet}}}

Selbst wenn die Infinitesimalrechnung eher mit Grenzwerten als mit Infinitesimalen entwickelt wird, ist es üblich, Symbole wie dx und dy so zu manipulieren, als wären sie reelle Zahlen; Obwohl es möglich ist, solche Manipulationen zu vermeiden, sind sie manchmal nicht sehr praktisch, um Operationen wie die Gesamtableitung auszudrücken.
Integralrechnung
Integralrechnung ist das Studium der Definitionen, Eigenschaften und Anwendungen von zwei verwandten Konzepten, dem unbestimmten Integral und dem bestimmten Integral. Der Prozess des Findens des Wertes eines Integrals wird Integration genannt. In der Fachsprache untersucht die Integralrechnung zwei verwandte lineare Operatoren.
Das unbestimmte Integral, auch Antiderivativ genannt, ist die inverse Operation zur Ableitung. F ist ein unbestimmtes Integral von f, wenn f eine Ableitung von F ist. (Diese Verwendung von Klein- und Großbuchstaben für eine Funktion und ihr unbestimmtes Integral ist in der Infinitesimalrechnung üblich.)
Das bestimmte Integral gibt eine Funktion ein und gibt eine Zahl aus, die die algebraische Summe der Flächen zwischen dem Graphen der Eingabe und der x-Achse ergibt. Die technische Definition des bestimmten Integrals beinhaltet die Grenze einer Summe von Flächen von Rechtecken, die als Riemannsche Summe bezeichnet wird.
Ein motivierendes Beispiel sind die in einer bestimmten Zeit zurückgelegten Strecken.
D i s t a n c e = S p e e d ⋅ T i m e {\displaystyle \mathrm {Distance} =\mathrm {Speed} \cdot \mathrm {Time} }

Wenn die Geschwindigkeit konstant ist, wird nur Multiplikation benötigt, aber wenn sich die Geschwindigkeit ändert, eine leistungsfähigere Methode zum Ermitteln der Entfernung ist erforderlich. Eine solche Methode besteht darin, die zurückgelegte Strecke zu approximieren, indem die Zeit in viele kurze Zeitintervalle aufgeteilt wird, dann die in jedem Intervall verstrichene Zeit mit einer der Geschwindigkeiten in diesem Intervall multipliziert wird und dann die Summe (eine Riemannsche Summe) der ungefähren zurückgelegten Strecke genommen wird in jedem Intervall. Die Grundidee ist, dass, wenn nur eine kurze Zeit vergeht, die Geschwindigkeit mehr oder weniger gleich bleibt. Eine Riemannsche Summe gibt jedoch nur eine Annäherung an die zurückgelegte Strecke. Wir müssen die Grenze aller solcher Riemann-Summen nehmen, um die genaue zurückgelegte Strecke zu finden.
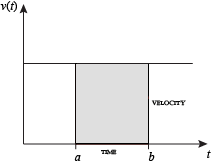

Wenn die Geschwindigkeit konstant ist, kann die über das angegebene Zeitintervall zurückgelegte Gesamtstrecke durch Multiplikation von Geschwindigkeit und Zeit berechnet werden. Wenn Sie beispielsweise 3 Stunden lang konstant 50 Meilen pro Stunde fahren, ergibt sich eine Gesamtstrecke von 150 Meilen. Wenn im Diagramm links konstante Geschwindigkeit und Zeit grafisch dargestellt werden, bilden diese beiden Werte ein Rechteck mit einer Höhe gleich der Geschwindigkeit und einer Breite gleich der verstrichenen Zeit. Daher berechnet das Produkt aus Geschwindigkeit und Zeit auch die rechteckige Fläche unter der (konstanten) Geschwindigkeitskurve. Diese Verbindung zwischen der Fläche unter einer Kurve und der zurückgelegten Strecke kann auf jeden unregelmäßig geformten Bereich ausgedehnt werden, der über einen bestimmten Zeitraum eine schwankende Geschwindigkeit aufweist. Wenn f(x) im Diagramm rechts die Geschwindigkeit darstellt, die sich im Laufe der Zeit ändert, ist die zurückgelegte Strecke (zwischen den durch a und b dargestellten Zeiten) die Fläche des schattierten Bereichs s.
Um diesen Bereich anzunähern, wäre eine intuitive Methode, den Abstand zwischen a und b in eine Anzahl gleicher Segmente aufzuteilen, wobei die Länge jedes Segments durch das Symbol Δx dargestellt wird. Für jedes kleine Segment können wir einen Wert der Funktion f (x) auswählen. Nennen Sie diesen Wert h. Dann ergibt die Fläche des Rechtecks mit Basis Δx und Höhe h die in diesem Segment zurückgelegte Strecke (Zeit Δx multipliziert mit der Geschwindigkeit h). Jedem Segment ist der Durchschnittswert der darüber liegenden Funktion zugeordnet, f(x) = h. Die Summe aller dieser Rechtecke ergibt eine Annäherung an die Fläche zwischen der Achse und der Kurve, die eine Annäherung an die zurückgelegte Gesamtstrecke darstellt. Ein kleinerer Wert für Δx ergibt mehr Rechtecke und in den meisten Fällen eine bessere Annäherung, aber für eine genaue Antwort müssen wir einen Grenzwert verwenden, wenn Δx sich Null nähert.
Das Symbol der Integration ist ∫ {\displaystyle \int }

, ein längliches S (das S steht für „Summe“). Das definite Integral wird geschrieben als: ∫ ein b f ( x ) d x. {\displaystyle \int _{a}^{b}f(x)\,dx.}

und wird gelesen „das Integral von a nach b von f-of-x in Bezug auf x.“ Die Leibniz-Notation dx soll vorschlagen, die Fläche unter der Kurve in eine unendliche Anzahl von Rechtecken zu teilen, so dass ihre Breite Δx die infinitesimal kleine dx wird. In einer auf Grenzwerten basierenden Formulierung des Kalküls ist die Notation
∫ a b ⋯ d x {\displaystyle \int _{a}^{b}\cdots \,dx}

als ein Operator zu verstehen, der eine Funktion als Eingabe nimmt und eine Zahl, die Fläche, als Ausgabe angibt. Das abschließende Differential dx ist keine Zahl und wird nicht mit f (x) multipliziert, obwohl es zur Erinnerung an die Δx-Grenzdefinition als solches in symbolischen Manipulationen des Integrals behandelt werden kann. Formal gibt das Differential die Variable an, über die die Funktion integriert ist, und dient als schließende Klammer für den Integrationsoperator.
Das unbestimmte Integral oder Antiderivativ wird geschrieben:
∫ f ( x ) d x. {\displaystyle {\displaystyle {\displaystyle {\displaystyle }}}.}
 ∫ 2 x d x = x 2 + C. {\displaystyle \int 2x\,dx=x^{2}+C.}
∫ 2 x d x = x 2 + C. {\displaystyle \int 2x\,dx=x^{2}+C.}

Die nicht spezifizierte Konstante C, die im unbestimmten Integral oder Antiderivativ vorhanden ist, wird als Integrationskonstante bezeichnet.
Fundamentalsatz
Der Fundamentalsatz der Analysis besagt, dass Differenzierung und Integration inverse Operationen sind. Genauer gesagt bezieht es die Werte von Antiderivativen auf bestimmte Integrale. Da es normalerweise einfacher ist, ein Antiderivativ zu berechnen, als die Definition eines bestimmten Integrals anzuwenden, bietet der Fundamentalsatz der Infinitesimalrechnung eine praktische Möglichkeit, bestimmte Integrale zu berechnen. Es kann auch als präzise Aussage darüber interpretiert werden, dass Differenzierung die Umkehrung der Integration ist.
Der Fundamentalsatz der Infinitesimalrechnung: Wenn eine Funktion f im Intervall stetig ist und wenn F eine Funktion ist, deren Ableitung f im Intervall (a, b) ist, dann
∫ abf ( x) d x = F ( b) − F ( a ) . {\displaystyle \int _{a}^{b}f(x)\,dx=F(b)-F(a).}

Ferner gilt für jedes x im Intervall (a, b)
d d x ∫ a x f ( t) d t = f ( x) . {\displaystyle {\frac {d}{dx}}\int _{a}^{x}f(t)\,dt=f(x).}
