gränser och infinitesimals
kalkyl utvecklas vanligtvis genom att arbeta med mycket små mängder. Historiskt sett var den första metoden att göra det av infinitesimals. Dessa är objekt som kan behandlas som reella tal men som i viss mening är ”oändligt små”. Till exempel, ett oändligt tal kan vara större än 0, men mindre än något tal i sekvensen 1, 1/2, 1/3,… och därmed mindre än något positivt reellt tal. Ur denna synvinkel är kalkyl en samling tekniker för att manipulera infinitesimaler. Symbolerna d x {\displaystyle dx}

och d y {\displaystyle dy}

togs för att vara oändliga, och derivatet d y / d x {\displaystyle dy/dx}

var helt enkelt deras förhållande.
den infinitesimal tillvägagångssätt föll i onåd i 19th century eftersom det var svårt att göra begreppet en infinitesimal exakt. Konceptet återupplivades emellertid i 20-talet med införandet av icke-standardanalys och smidig infinitesimal analys, vilket gav solida grunder för manipulering av infinitesimaler.
i slutet av 19th century, infinitesimals ersattes inom akademin av epsilon, delta approach to limits. Gränser beskriver värdet på en funktion vid en viss ingång i termer av dess värden vid närliggande ingångar. De fångar småskaligt beteende i samband med det verkliga talsystemet. I denna behandling är kalkyl en samling tekniker för att manipulera vissa gränser. Infinitesimals ersätts av mycket små tal, och funktionens oändligt små beteende hittas genom att ta det begränsande beteendet för mindre och mindre tal. Gränser ansågs ge en mer rigorös grund för kalkyl, och av denna anledning blev de standardmetoden under det tjugonde århundradet.
differentialkalkyl

differentialkalkyl är studien av definitionen, egenskaperna och tillämpningarna av derivatet av en funktion. Processen att hitta derivatet kallas differentiering. Med tanke på en funktion och en punkt i domänen är derivatet vid den punkten ett sätt att koda funktionens småskaliga beteende nära den punkten. Genom att hitta derivatet av en funktion vid varje punkt i dess domän är det möjligt att producera en ny funktion, kallad derivatfunktionen eller bara derivatet av den ursprungliga funktionen. I formella termer är derivatet en linjär operatör som tar en funktion som ingång och producerar en andra funktion som utgång. Detta är mer abstrakt än många av de processer som studeras i elementär algebra, där funktioner vanligtvis matar in ett tal och matar ut ett annat nummer. Till exempel, om fördubblingsfunktionen ges ingången tre, matar den ut sex, och om kvadreringsfunktionen ges ingången tre, matar den ut nio. Derivatet kan dock ta kvadreringsfunktionen som en ingång. Detta innebär att derivatet tar all information om kvadreringsfunktionen—som att två skickas till fyra, tre skickas till nio, fyra skickas till sexton och så vidare—och använder denna information för att producera en annan funktion. Funktionen som produceras genom att härleda kvadreringsfunktionen visar sig vara fördubblingsfunktionen.
i mer uttryckliga termer kan ”fördubblingsfunktionen” betecknas med g(x) = 2x och ”kvadreringsfunktionen” med f(x) = x2. ”Derivatet” tar nu funktionen f(x), definierad av uttrycket ”x2”, som en ingång, det vill säga all information—som att två skickas till fyra, tre skickas till nio, fyra skickas till sexton och så vidare—och använder denna information för att mata ut en annan funktion, funktionen g (x) = 2x, som kommer att visa sig.
den vanligaste symbolen för ett derivat är ett apostrofliknande märke som heter prime. Således betecknas derivatet av en funktion som kallas f med f’, uttalad ”f prime”. Till exempel, om f(x) = x2 är kvadreringsfunktionen, är f'(x) = 2x dess derivat (fördubblingsfunktionen g ovanifrån). Denna notation är känd som Lagrange notation.
om inmatningen av funktionen representerar tid, representerar derivatet förändring med avseende på tid. Till exempel, om f är en funktion som tar en tid som ingång och ger positionen för en boll vid den tiden som utgång, är derivatet av f Hur positionen förändras i tid, det vill säga det är bollens hastighet.
om en funktion är linjär (det vill säga om grafen för funktionen är en rak linje), kan funktionen skrivas som y = mx + b, där x är den oberoende variabeln, y är den beroende variabeln, b är y-avlyssningen och:
m = rise run = förändring i y förändring i x = VR Y X . {\displaystyle m={\frac {\text {rise}} {\text{run}}} = {\frac {{\text{Ändra i }}y} {{\text {Ändra i }}x}} = {\frac {\Delta y} {\Delta x}}.}

detta ger ett exakt värde för lutningen på en rak linje. Om grafen för funktionen inte är en rak linje varierar förändringen i y dividerat med förändringen i x. Derivat ger en exakt betydelse för begreppet förändring i produktionen med avseende på förändring i input. För att vara konkret, låt f vara en funktion och fixa en punkt a i domänen f. (a, f(A)) är en punkt på funktionens graf. Om h är ett tal nära noll, är a + h ett tal nära a. därför är (a + h, f (A + h)) nära(a, f (a)). Lutningen mellan dessa två punkter är
m = f ( a + h ) − f ( a ) ( a + h ) − a = f ( a + h ) − f ( a ) h . {\displaystyle m={\frac {f (a + h)-f(a)} {(a+h)-a}}={\frac {f(a+h) – f(a)} {h}}.}

detta uttryck kallas en skillnadskvotient. En linje genom två punkter på en kurva kallas en sekant linje, så m är lutningen på sekantlinjen mellan(A, f (A)) och(a + h, f (a + h)). Secant-linjen är bara en approximation till funktionens beteende vid punkten A eftersom den inte tar hänsyn till vad som händer mellan A och A + h. det är inte möjligt att upptäcka beteendet vid A genom att ställa in h till noll eftersom detta skulle kräva delning med noll, vilket är odefinierat. Derivatet definieras genom att ta gränsen som h tenderar till noll, vilket innebär att det tar hänsyn till f: s beteende för alla små värden på h och extraherar ett konsekvent värde för fallet när h är lika med noll:
lim h 0 f ( a + h ) − f ( a ) h . {\displaystyle \ lim _{h \ till 0}{f (A + h) – f(A) \over {h}}.}

geometriskt är derivatet lutningen på tangentlinjen till grafen av f Vid a. tangentlinjen är en gräns för sekantlinjer precis som derivatet är en gräns för skillnadskvotienter. Av detta skäl kallas derivatet ibland funktionens lutning f.
Här är ett särskilt exempel, derivatet av kvadratfunktionen vid ingången 3. Låt f (x) = x2 vara kvadreringsfunktionen.

f ′ ( 3 ) = lim h → 0 ( 3 + h ) 2 − 3 2 h = lim h → 0 9 + 6 h + h 2 − 9 h = lim h → 0 6 h + h 2 h = lim h → 0 ( 6 + h ) = 6 {\displaystyle {\begin{aligned}f'(3)&=\lim _{h\to 0}{(3+h)^{2}-3^{2} \over {h}}\\&=\lim _{h\to 0}{9+6h+h^{2}-9 \over {h}}\\&=\lim _{h\to 0}{6h+h^{2} \over {h}}\\&=\lim _{h\to 0}(6+h)\\&=6\end{aligned}}}

tangentlinjens lutning till kvadratfunktionen vid punkten (3, 9) är 6, det vill säga, Det går upp sex gånger så fort som det går till höger. Gränsprocessen som just beskrivits kan utföras för vilken punkt som helst i domänen för kvadratfunktionen. Detta definierar derivatfunktionen för kvadratfunktionen eller bara derivatet av kvadratfunktionen för kort. En beräkning som liknar den ovan visar att derivatet av kvadratfunktionen är fördubblingsfunktionen.
Leibniz notation
en vanlig notation, introducerad av Leibniz, för derivatet i exemplet ovan är
y = x 2 d y d x = 2 x . {\displaystyle {\begin{justerad}y&=x^{2}\\{\frac {dy}{dx}}&=2x.\end{justerad}}}

i ett tillvägagångssätt baserat på gränser ska symbolen dy / dx tolkas inte som kvoten för två siffror utan som en stenografi för gränsen beräknad ovan. Leibniz hade dock för avsikt att representera kvoten av två oändligt små tal, dy är den oändligt små förändringen i y orsakad av en oändligt liten förändring dx applicerad på x. Vi kan också tänka på d/dx som en differentieringsoperatör, som tar en funktion som en ingång och ger en annan funktion, derivatet, som utgången. Till exempel:
d d x ( x 2 ) = 2 x . {\displaystyle {\frac {d}{dx}} (x^{2})=2x.}

i denna användning läses DX i nämnaren som ”med avseende på x”. Ett annat exempel på korrekt notering kan vara:
g ( T ) = T 2 + 2 t + 4 d d T g ( T ) = 2 T + 2 {\displaystyle {\begin{justerad}g(T)=T^{2}+2t+4\\\\{D \over dt}g(t)=2t+2\end{justerad}}}

även när kalkyl utvecklas med hjälp av gränser snarare än infinitesimaler, är det vanligt att manipulera symboler som dx och dy som om de var reella tal; även om det är möjligt att undvika sådana manipuleringar, är de ibland notationellt lämpliga för att uttrycka operationer som det totala derivatet.
integralkalkyl
integralkalkyl är studien av definitioner, egenskaper och tillämpningar av två relaterade begrepp, den obestämda integralen och den bestämda integralen. Processen att hitta värdet av en integral kallas integration. På tekniskt språk studerar integralkalkyl två relaterade linjära operatörer.
den obestämda integralen, även känd som antiderivativ, är den inversa operationen till derivatet. F är en obestämd integral av f när f är ett derivat av F. (Denna användning av små och stora bokstäver för en funktion och dess obestämda integral är vanligt i kalkyl.)
den bestämda integralen matar in en funktion och matar ut ett tal, vilket ger den algebraiska summan av områden mellan grafen för ingången och x-axeln. Den tekniska definitionen av den bestämda integralen innebär gränsen för en summa av rektanglar, kallad en Riemann-summa.
ett motiverande exempel är de avstånd som reste under en viss tid.
d i S t A N c E = S P e E d t I m e {\displaystyle \mathrm {Distance} =\mathrm {Speed} \cdot \mathrm {Time} }

Om hastigheten är konstant behövs endast multiplikation, men om hastigheten ändras krävs en kraftfullare metod för att hitta avståndet. En sådan metod är att approximera avståndet som reste genom att bryta upp tiden i många korta tidsintervaller, sedan multiplicera tiden som förflutit i varje intervall med en av hastigheterna i det intervallet och sedan ta summan (en Riemann-summa) av det ungefärliga avståndet som reste i varje intervall. Grundtanken är att om bara en kort tid går, kommer hastigheten att förbli mer eller mindre densamma. En Riemann-summa ger emellertid bara en approximation av det tillryggalagda avståndet. Vi måste ta gränsen för alla sådana Riemann-summor för att hitta det exakta avståndet som reste.
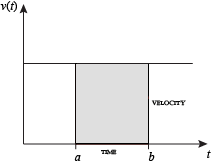

när hastigheten är konstant kan det totala avståndet som reste över det angivna tidsintervallet beräknas genom att multiplicera hastighet och tid. Till exempel, att resa en stadig 50 mph i 3 timmar resulterar i ett totalt avstånd på 150 miles. I diagrammet till vänster, när konstant hastighet och tid ritas, bildar dessa två värden en rektangel med höjd lika med hastigheten och bredden lika med den tid som förflutit. Därför beräknar produkten av hastighet och tid också det rektangulära området under (konstant) hastighetskurvan. Denna anslutning mellan området under en kurva och sträcka kan förlängas till varje oregelbundet formad region som uppvisar en fluktuerande hastighet under en given tidsperiod. Om f (x) i diagrammet till höger representerar hastighet eftersom det varierar över tiden, är det avstånd som reste (mellan de tider som representeras av A och b) området för det skuggade området s.
för att approximera det området skulle en intuitiv metod vara att dela upp avståndet mellan A och b i ett antal lika segment, längden på varje segment som representeras av symbolen Bisexx. För varje litet segment kan vi välja ett värde på funktionen f (x). Ring det värdet h. då området av rektangeln med bas-Ubix och höjd h ger avståndet (tid Ubix multiplicerat med hastighet h) reste i det segmentet. Associerat med varje segment är medelvärdet av funktionen ovanför den, f(x) = h. summan av alla sådana rektanglar ger en approximation av området mellan axeln och kurvan, vilket är en approximation av det totala avståndet som reste. Ett mindre värde för Jacobx kommer att ge fler rektanglar och i de flesta fall en bättre approximation, men för ett exakt svar måste vi ta en gräns när Jacobx närmar sig noll.
integrationssymbolen är {\displaystyle \ int }

, en långsträckt S (S står för”summa”). Den bestämda integralen är skriven som: a b f ( x ) D x . {\displaystyle \ int _{a}^{b}f (x)\, dx.}

och läses ”integralet från A till b av f-Of-x med avseende på x.” Leibniz-notationen dx är avsedd att föreslå att området under kurvan delas in i ett oändligt antal rektanglar, så att deras bredd Jacobx blir den oändligt lilla dx. I en formulering av kalkylen baserad på gränser ska notationen
kubi a b DX {\displaystyle \ int _ {a}^{b} \ cdots \, dx}

förstås som en operatör som tar en funktion som en ingång och ger ett tal, området, som en utgång. Den avslutande differentialen, dx, är inte ett tal och multipliceras inte med f(x), även om den tjänar som en påminnelse om definitionen av gräns för gräns för Gräns, den kan behandlas som sådan i symboliska manipulationer av integralet. Formellt indikerar differentialen variabeln över vilken funktionen är integrerad och fungerar som en stängningsfäste för integrationsoperatören.
den obestämda integralen, eller antiderivativ, är skriven:
kub f ( x ) D x . {\displaystyle \ int f (x)\, dx.}

funktioner som endast skiljer sig från en konstant har samma derivat, och det kan visas att antiderivativet för en given funktion faktiskt är en familj av funktioner som endast skiljer sig från en konstant. Eftersom derivatet av funktionen y = x2 + C, där C är vilken som helst konstant, är y’ = 2x, ges antiderivativet av den senare med:
2 x D x = x 2 + c . {\displaystyle \ int 2x\,dx=x^{2}+C.}

den ospecificerade konstanten C som finns i den obestämda integralen eller antiderivativ kallas integrationens konstant.
Fundamental theorem
den grundläggande theorem of calculus säger att differentiering och integration är inversa operationer. Mer exakt relaterar det värdena på antiderivativ till bestämda integraler. Eftersom det vanligtvis är lättare att beräkna en antiderivativ än att tillämpa definitionen av en bestämd integral, ger den grundläggande satsen för kalkyl ett praktiskt sätt att beräkna bestämda integraler. Det kan också tolkas som ett exakt uttalande om att differentiering är inversen av integration.
den grundläggande sats av kalkyl stater: Om en funktion f är kontinuerlig på intervallet och om F är en funktion vars derivat är f på intervallet (a, b), då
a b f ( x ) D x = F ( b ) − F ( A ) . {\displaystyle \ int _{a}^{b}f (x)\, dx=F(b)-F (A).}

dessutom, för varje x i intervallet (a, b),
d d x cu x f ( t ) d t = f ( x ) . {\displaystyle {\frac {d}{dx}}\int _{a}^{x}f(t)\, dt=f (x).}

denna insikt, gjord av både Newton och Leibniz, som baserade sina resultat på tidigare arbete av Isaac Barrow, var nyckeln till spridningen av analytiska resultat efter att deras arbete blev känt. Den grundläggande satsen ger en algebraisk metod för att beräkna många bestämda integraler – utan att utföra gränsprocesser-genom att hitta formler för antiderivativ. Det är också en prototyplösning av en differentialekvation. Differentialekvationer relaterar en okänd funktion till dess derivat och är allestädes närvarande inom vetenskapen.