nemrégiben a 0 meghatározásának különböző igazolásaira gondoltam! (factorial nulla) ami
$0!=1$$
az 1 feltételezett értéke nyilvánvalónak tűnhet, ha figyelembe vesszük a rekurzív képletet. Ez azonban nem elégített ki “matematikailag”. Ezért döntöttem úgy, hogy megírom ezt a néhány mondatot. Motivációkat adok a kevésbé fejletteknek, de motivációk is lesznek valamivel több bennfentes számára.
⭐️Faktoriális a Skalár Kalkulátor

⭐️ Faktoriális, valamint ismételt
Az integer n > 0 faktoriális meghatározása a következő
$$n!=n \ times (n-1)\times (n-2) \times \ldots\times 2 \ times 1$$
könnyedén láthatja, hogy az alábbiakban rekurzív képlet következik
$$n!=n \ times (n-1)!$ $
$1!=1$$
⭐️ 0! = 1-motiváció a
$n kis transzformációja alapján!=n \ times (n-1)!$$
AD
$$(n-1)!= \ frac{n!}{n}$$
helyettesítve n = 1
$(1-1)!= \ frac{1!}{1}$$
$0!=1!=1$$
Ez a magyarázat, bár könnyű, nem nyújt (véleményem szerint) elég mély megértést arról, hogy “miért kell ez a legjobb megoldás”.
⭐️ Factorial n! számít a lehetséges különböző sorozatok az n különböző tárgyak (permutációk)
tegyük fel, hogy van egy meghatározott tartalmazó, n elemek
$$\{1,2,\ldots,n\}$$
Most let”s gróf lehetséges rendelési elemek ez set
- n módon kiválasztása első elem (mert mi az egész beállítás áll rendelkezésre)
- n-1 módon kiválasztja a második elem (mert az első volt kiválasztva, van n-1 balra)
- n-2 módon kiválasztása harmadik elem (mert a kettő már kiválasztott, vagy n-2)
- …
- n- (k-1) módon kiválasztása elem száma k (mert a k-1 már kiválasztott, n- (k-1) marad)
- 2 módon kiválasztása elem száma n-1. (mert a n-2 a kiválasztott, még 2 van hátra)
- 1 mód kiválasztása elem száma n (mert az n-1 volt a kiválasztott, nem maradt, csak egy)
Végre számolni az összes lehetséges módon, kapunk
$$n\alkalommal (n-1)\times (n-2)\times \ldots \alkalommal 2\alkalommal 1=n!$$
következtetés: az N faktoriális számolja az n elemeket tartalmazó halmaz permutációjának számát.
⭐️ k-permutációk n néha részleges permutációk, vagy variációk
A k-permutációk n a különböző megrendelt megállapodások egy k-elem, részhalmaz, hogy egy n-készlet. Az ilyen n k-permutációk száma
$$p_k^n = n \ times (n-1)\times (n-2)\times\ldots \times\bigg(n-(K-1) \bigg) = \ FRAC{n!{(n-k)!} $$
könnyű belátni, hogy az n-permutáció permutáció, tehát
$p_n^n = n!$$
$$n! = \ frac{n!{(n-n)!= \ frac{n!}{0!} $$
a következő betekintést miért 0!=1 a helyes meghatározás származik, hogy minden n > 0 mi kell
$0! \ times n! = n!$$
⭐️ a Funkciója, mint egy beállítja feltérképezése

Függvény
$$f:A\to B$$
Függvény f : A → B, ahol minden a ∈ Egy van f(a) = b ∈ B, meghatározza a kapcsolat elemek, valamint b. Azt mondhatjuk, hogy az elemek a ∈ A, b ∈ B kapcsolatos “f” ha pedig csak akkor, ha f(a) = b.
⭐️ függvény, mint egy részhalmaza derékszögű termék
függvény egy bináris kapcsolat, ami azt jelenti, függvény lehet kifejezni egy részhalmaza egy derékszögű termék.
$$(a,b)\f \subseteq Egy\alkalommal B \iff f(a)=b$$
⭐️ Injektív függvény

Injektív függvény egy olyan funkció, amely megőrzi a megkülönböztethetőség: soha nem térképek különböző elemeit domain ugyanazon eleme a codomain. Röviden
$x\neq y \Rightarrow f(x) \neq f(y)$
⭐️ Surjective funkció

a függvény F surjective (vagy rá) ha minden elem B codomain, van legalább egy elem a tartományban olyan, hogy f(A)=B . Nem szükséges, hogy x egyedi legyen.
$f:A\B$$
$${\nagyméretű \displaystyle\forall_{b, \a, B} \quad\displaystyle\exists_{a\a}\quad}f(a)=b$$
⭐️ Bijective funkció

Bijective funkció, vagy egy-egy levelezést, egy olyan funkció, ahol minden elem egy meghatározott párosított pontosan egy eleme, a másik meg, minden eleme a másik meg párosított pontosan egy eleme, az első szettet. Nincsenek párosítatlan elemek.
A matematikai kifejezések, egy bijective funkció mindkét injektív, valamint surjective feltérképezése a készlet Egy meghatározott B.
⭐️ Bijective funkció vs Permutáció
Permutáció egy olyan funkció, hogy visszatér érdekében állítsa be, azaz, ha figyelembe vesszük, hogy a n-elem állítva {1, 2, …, n}, akkor permutáció lesz funkció
$$p:\{1, 2, …, n\}\a\{1, 2, …, n\}$$
lehetőség a bijective funkció állapotát.
a permutációk számáról való megkérdezéssel ugyanúgy feltehetjük a kérdést, hogy egy adott készletből hány különböző bijektum van önmagában.
⭐️ üres függvény
egy üres függvény minden olyan függvény, amelynek tartománya üres készlet.
$f:\emptyset\to B$$
az üres “chart” függvény egy üres halmaz, mivel a domain és a codomain Descartesiai terméke üres.
$ \ emptyset \ times B = \ emptyset$$
az üres funkció megőrzi a megkülönböztetést (injective), mert a tartományban (egy üres készlet) nincs két különböző elem, amelyekre a funkció értéke egyenlő.
⭐️ egy üres függvény speciális esete
elemezzük azt a függvényt, amely üresen leképezi a
$ f:\ emptyset \ to \ emptyset$$
egy ilyen függvény egy bijection, mert injective függvény (mint fent látható), és nincs elem codomain (a codomain egy üres készlet), amely nem áll kapcsolatban az elemek a domain.
Felhívjuk figyelmét, hogy pontosan van egy ilyen bijection, amely az eredménye, hogy a függvény egy részhalmaza a derékszögű termék domain és codomain. Ebben az esetben ez csak egy lehetséges készlet.
$f:\ emptyset \ to \ emptyset$ $
$ \ emptyset \ times \ emptyset = \ emptyset$ $
az üres készletnek pontosan egy részhalmaza van, ami az üres készlet – így egy ilyen bijection egyedileg definiált.
⭐️ 0! = 1 vs üres függvény
fent írtam, hogy az n-elemkészlet permutációinak száma megegyezik az ebből a készletből származó különálló bijektív függvények számával.
Following-a permutáció 0-elem készlet megfelel a bijection egy üres készlet az üres készlet /
a különleges eset üres függvény csak 1 – és bemutattam a bizonyíték arra, hogy létezik csak egy ilyen funkció 🙂
elég mély betekintést miért 0! kellene 1.
⭐️ A gamma-függvény
a matematikában a Gamma-függvény a faktoriális függvény egyik kiterjesztése, amelynek argumentuma 1-gyel lefelé tolódik, valós és összetett számokra.
$\Gamma(z)=\displaystyle\int_0^{+\infty}t^{z-1}E^{-t}dt$
az alkatrészek integrálása után megkapjuk a rekurzív képletet
$\Gamma (z + 1)=z\cdot\Gamma(z)$$
$$\Gamma(1)=?$$
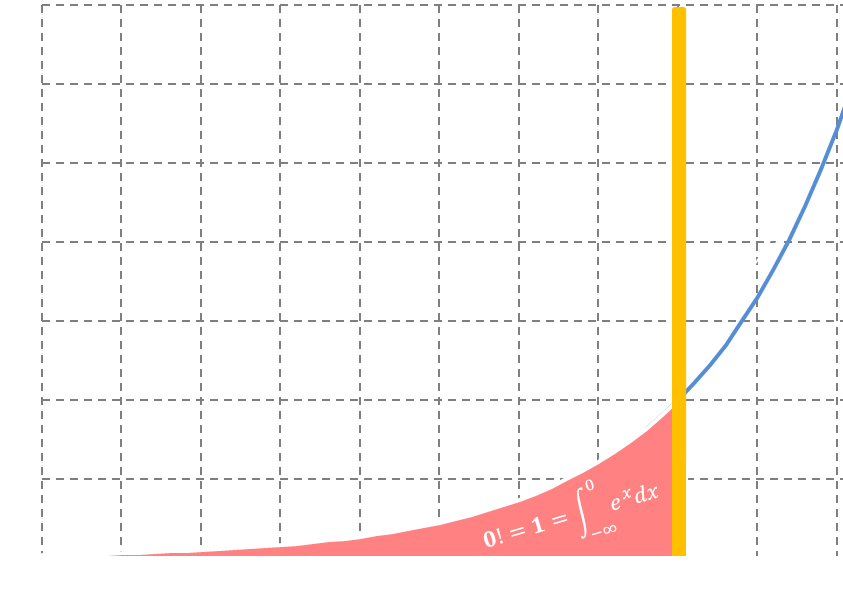
$\Gamma(1)=\displaystyle\int_0^{+\infty}e^{-t}DT=\displaystyle\int_ {- \infty}^{0}E^{t}dt$
$$ \ Gamma(n+1)=n!$$
$0! = \Gamma(1) = 1$$
⭐️ Scalar support for the Gamma function

Functions in Scalar Calculator, that support Gamma special function
- Gamma(x) – Gamma special function Γ(s)
- sgnGamma(x) – Signum of Gamma special function, Γ(s)
- logGamma(x) – Log Gamma special function, lnΓ(s)
- diGamma(x) – Digamma function as the logarithmic derivative of the Gamma special function, ψ(x)
- GammaL(s,x) – Lower incomplete gamma special function, γ(s,x)
- GammaU(s,x) – Upper incomplete Gamma special function, Γ(s,x)
- GammaP(s,x) , GammaRegL(s,x) – Lower regularized P gamma special function, P(s,x)
- GammaQ(s,x), GammaRegU(s,x) – Upper regularized Q Gamma special function, Q(s,x)
Gamma function chart

Gamma function vs Factorial chart

⭐️ E szám és faktoriális reláció
Az E^x Taylor sorozatának kiterjesztése alapján könnyű megmutatni, hogy
$$e= \ displaystyle \ sum_{n = 0}^ \ infty \ frac{1}{n!} = \ frac{1}{0!} + \ frac{1} {1!} + \ frac{1} {2!} + \ frac{1}{3!}+\ldots$$
Sequence convergence

This is fascinating, as it shows even stronger relation of factorial to e
Thanks for reading! All the best 🙂