Matek

a differenciálszámítás egy függvény deriváltjának definícióját, tulajdonságait és alkalmazásait vizsgálja. A származék megtalálásának folyamatát differenciálásnak nevezik. Egy függvény és egy pont a tartományban, a derivált ezen a ponton egy módja a kódolás a kis léptékű viselkedését a függvény közelében, hogy pont. Ha egy függvény származékát a tartomány minden pontján megtalálja, akkor új függvényt hozhat létre, amelyet származékos függvénynek vagy csak az eredeti függvény származékának neveznek. Formális értelemben a derivált egy lineáris operátor, amely bemenetként egy függvényt vesz fel, kimenetként pedig egy második függvényt állít elő. Ez elvontabb, mint az elemi algebrában vizsgált folyamatok közül sok, Ahol a függvények általában egy számot adnak be, és egy másik számot adnak ki. Például, ha a duplázó függvény A három bemenetet kapja, akkor hat kimenetet ad ki, ha pedig a négyzetes függvény A három bemenetet kapja, akkor kilencet ad ki. A származék azonban a négyzetfüggvényt bemenetként veheti fel. Ez azt jelenti, hogy a származékos veszi az összes információt a négyszögesítése funkció—például, hogy két küldött négy, három küldött kilenc, négy küldött tizenhat, stb.—használja ezt az információt, hogy készítsen egy másik funkció. A négyzetes függvény létrejöttével létrejövő függvény a duplázó függvény.

explicitebben kifejezve a” duplázó függvényt “g(x) = 2x, a” négyzetes függvényt ” F(x) = x2 jelölheti. A “derivált” most az “x2” kifejezés által definiált f(x) függvényt veszi bemenetként, azaz az összes információt—például azt, hogy kettőt négyre küldünk, hármat kilencre küldünk, négyet tizenhat—ra küldünk, és így tovább -, és ezt az információt egy másik funkció, a g(x) = 2x függvény kimenésére használja, amint kiderül.

a származék leggyakoribb szimbóluma egy aposztrófszerű jel, amelyet prime-nak hívnak. Így az f nevű függvény származékát f ‘ jelöli, kiejtve “f prime”. Például, ha f (x) = x2 a négyzetes függvény, akkor f'(x) = 2x a származéka (a duplázó függvény g felülről). Ezt a jelölést Lagrange jelölésének nevezik.

Ha a függvény bemenete időt jelent, akkor a derivált az időhöz viszonyított változást jelenti. Például, ha f egy olyan függvény, amely bemenetként időt vesz igénybe, és egy golyó helyzetét adja abban az időben kimenetként, akkor az f származéka az, hogy a pozíció időben változik, vagyis a labda sebessége.

Ha egy függvény lineáris (vagyis ha a függvény grafikonja egyenes vonal), akkor a függvény y = mx + b, ahol x a független változó, y a függő változó, b az y-elfogó, és:

m = rise run = változás y változásban x = Δ y Δ X . {\displaystyle m = {\FRAC {\text {rise}}} {\text {run}}}}}}} = {\FRAC {\text{change in}}}}}} {\FRAC {\Delta y} {\Delta x}}}}}}.}

Ez pontos értéket ad egy egyenes meredekségének. Ha a függvény grafikonja nem egyenes vonal, akkor az y változása osztva az x változásával. A származtatott ügyletek pontos jelentést adnak a kibocsátás változásának fogalmához a bemenet változása tekintetében. Ahhoz, hogy konkrét legyen, legyen f függvény, és rögzítsen egy a pontot az f tartományában. (a, f (a)) egy pont a függvény grafikonján. Ha h egy nullához közeli szám, akkor a + h egy A-hoz közeli szám. ezért (a + h, f (a + h)) közel van (a, f(a))). A két pont közötti lejtés

m = f (a + h) − f ( a) (a + h ) − A = f ( a + h) – f ( a) h . {\displaystyle m = {\frac {f (a + h)-f(a)} {(a+h)-a}}={\frac {F(a+h) – f(a)} {h}}}.}

ezt a kifejezést különbség hányadosnak nevezik. A görbe két pontján átmenő vonalat metszővonalnak nevezzük, tehát m a metszővonal lejtése (a, f(a) és (a + h, f(a + h) között). A secant vonal csak egy közelítés a viselkedését a függvény az a pont, mert nem veszi figyelembe, hogy mi történik az a és a + h. nem lehetséges, hogy felfedezzék a viselkedés a beállításával h nullára, mert ez lenne szükség elosztjuk nulla, amely meghatározatlan. A származékos határozza meg, figyelembe véve a határ, mint h hajlamos arra, hogy nulla, ami azt jelenti, hogy úgy véli, a viselkedés f minden kis értékek h kivonatok következetes érték az esetet, amikor a h nullával egyenlő:

lim h → 0 f ( a + h ) − f ( a ) h . {\displaystyle \ lim _ {h \ to 0}{f (a + h) – f(a) \over {h}}}.}

geometriailag, a származék az érintővonal lejtése az f grafikonjához a. az érintővonal a metszővonalak határa, ugyanúgy, mint a származék a különbség hányadosainak határa. Ezért a származékot néha az f függvény lejtőjének nevezik.

itt van egy konkrét példa, a négyzetfüggvény származéka a 3 bemeneten. Legyen f (x) = x2 a négyzetfüggvény.

egy görbe F ” (x) származéka az adott ponton az adott görbével érintkező vonal lejtése. Ezt a lejtést úgy határozzák meg, hogy figyelembe veszik a metszővonalak lejtőinek korlátozó értékét. Itt az érintett funkció (piros színnel rajzolva) f(x) = x3 − x. az érintővonal (zölden), amely áthalad a ponton (-3/2, -15/8), 23/4 lejtéssel rendelkezik. Vegye figyelembe, hogy a kép függőleges és vízszintes skálái eltérőek.

f ′ ( 3 ) = lim h → 0 ( 3 + h ) 2 − 3 2 h = lim h → 0 9 + 6 h + h 2 − 9 h = lim h → 0 6 h + h 2 h = lim h → 0 ( 6 + h ) = 6 {\displaystyle {\begin{aligned}f'(3)&=\lim _{h\to 0}{(3+h)^{2}-3^{2} \over {h}}\\&=\lim _{h\to 0}{9+6h+h^{2}-9 \over {h}}\\&=\lim _{h\to 0}{6h+h^{2} \over {h}}\\&=\lim _{h\to 0}(6+h)\\&=6\end{aligned}}}

a lejtőn A érintője, hogy a művészet funkciója a pont (3, 9), 6, azaz, fel hatszor olyan gyorsan, mint az igaz. Az éppen leírt határfolyamat a négyzetes függvény tartományának bármely pontjára végrehajtható. Ez határozza meg a négyzetes függvény derivált funkcióját, vagy röviden csak a négyzetes függvény deriváltját. A fentihez hasonló számítás azt mutatja, hogy a négyzetes függvény deriváltja a duplázó függvény.

Leibniz jelölés

a Leibniz által bevezetett közös jelölés a fenti példában szereplő származékra

y = x 2 d y d x = 2 x. {\displaystyle {\begin{igazított}y&=x^{2}\{\frac {dy}{dx}}&=2x.\end{igazított}}}}}

a határértékeken alapuló megközelítésben a dy/dx szimbólumot nem két szám hányadosaként kell értelmezni, hanem a fent kiszámított határ gyorsírásaként. Leibniz azonban tervezem, hogy képviselje a hányadost két elképzelhetetlenül kicsi számok, dy, hogy a elképzelhetetlenül csekély változás y okozta egy elképzelhetetlenül csekély változás dx alkalmazni x. Azt is hiszem, hogy a d/dx, mint a differenciálás üzemeltető, ami a funkciója, mint a bemeneti, illetve adja, másik funkció, a származékos, a kimenet. Például:

d D x (x 2) = 2 x . {\displaystyle {\frac {d}{dx}}(x^{2})=2x.}

ebben A használat, a dx a nevező olvasni, mint “tekintetében x”. A helyes jelölés másik példája lehet:

g ( t ) = t 2 + 2 t + 4 d d t g ( t ) = 2 t + 2 {\displaystyle {\begin{igazítva}g(t)=t^{2}+2t+4\\\\{d \vége dt}g(t)=2t+2\end{igazítva}}}

Még akkor is, amikor a matematika fejlesztett korlátok helyett infinitesimals, gyakori, hogy manipulálják a szimbólumok, mint a dx, valamint dy, mintha valós számok; bár lehetséges, hogy elkerüljék az ilyen manipulációk, ezek néha notationally kényelmes kifejező műveletek, mint a teljes származék.

integrálni

integrálni a tanulmány a fogalmak, tulajdonságok, alkalmazások, valamint a két kapcsolódó fogalmak, a határozatlan integrál, illetve a határozott integrál. Az integrál értékének megtalálásának folyamatát integrációnak nevezik. MŰSZAKI nyelven az integral calculus két kapcsolódó lineáris operátort vizsgál.

a határozatlan integrál, más néven az antiderivatív, a származék inverz művelete. F az F határozatlan integrálja, ha f az F származéka. (A függvény alsó és felsőbetűinek és határozatlan integráljának használata gyakori a kalkulusban.)

a határozott integrál bemenet egy függvényt és egy számot ad ki, amely a bemenet és az x tengely grafikonja közötti területek algebrai összegét adja meg. A határozott integrál technikai meghatározása magában foglalja a téglalapok összegének határát, amelyet Riemann-összegnek neveznek.

motiváló példa az adott időben megtett távolságok.

D I S T A n c E = S P e D ⋅ T I m e {\displaystyle \mathrm {Distance} =\mathrm {Speed} \cdot \mathrm {Time} }

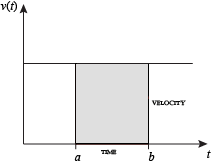
Ha a sebesség állandó, akkor az adott időintervallumban megtett teljes távolság szorzási sebességgel és idővel számítható ki. Például egy állandó 50 mph utazás 3 órán keresztül 150 mérföld teljes távolságot eredményez. A bal oldali ábrán, amikor állandó sebességet és időt ábrázolunk, ez a két érték egy téglalapot képez, amelynek magassága megegyezik az eltelt idővel megegyező sebességgel és szélességgel. Ezért a sebesség és az idő szorzata az (állandó) sebességgörbe alatti téglalap alakú területet is kiszámítja. Ez a kapcsolat a görbe alatti terület és a megtett távolság között bármely szabálytalan alakú régióra kiterjeszthető, amely egy adott időtartam alatt ingadozó sebességet mutat. Ha az f (x) A jobb oldali ábrán a sebességet jelöli, mivel az idővel változik, a megtett távolság (az A és b által képviselt idők között) az árnyékolt régió területe s.

az adott terület közelítéséhez intuitív módszer az A és b közötti távolság felosztása több egyenlő szegmensre, az egyes szegmensek hossza, amelyet a Δx szimbólum képvisel. Minden kis szegmens esetében kiválaszthatjuk az f(x) függvény egyik értékét. Hívja ezt az értéket h. ezután a téglalap területe Δx bázissal és H magassággal megadja az adott szegmensben megtett távolságot (Δx szorozva h sebességgel). Az egyes szegmensekhez társítva a fenti függvény átlagos értéke, f (x) = h. az összes ilyen téglalap összege közelíti a tengely és a görbe közötti területet, ami a teljes megtett távolság közelítése. A Δx kisebb értéke több téglalapot ad, a legtöbb esetben jobb közelítést, de a pontos válaszhoz határértéket kell vennünk, mivel az Δx megközelíti a nullát.

az integráció szimbóluma ∫ {\displaystyle \ int }

, egy hosszúkás S (az S jelentése “sum”). A határozott integrál a következőképpen íródott: ∫ a b f (x) D x . {\displaystyle \ int _ {a}^{b}f (x)\, dx.}

és olvasható “az integrál A-tól B-ig az F-of-x tekintetében x.” a Leibniz jelölés dx célja, hogy azt sugallják, elosztjuk a terület a görbe alatt egy végtelen számú téglalapok, úgy, hogy azok szélessége Δx lesz a végtelenül kis DX. A limiteken alapuló kalkulus megfogalmazásakor a

∫ A b ⋯ D x {\displaystyle \ int _ {a}^{b} \ cdots \, dx}

olyan operátornak kell tekinteni, amely bemenetként vesz egy függvényt, és megadja a területet, mint kimenetet. A záró differenciál, a dx nem szám, és nem szorozza meg f(x), bár az Δx határmeghatározás emlékeztetőjeként az integrál szimbolikus manipulációiban ilyenként kezelhető. Formálisan a differenciálmű jelzi azt a változót, amelyre a függvény integrálva van, záróelemként szolgál az integrációs operátor számára.

a határozatlan integrál, vagy antiderivatív, van írva:

f f (x ) D x . {\displaystyle \ int f (x)\, dx.}

A csak egy állandóval eltérő függvények azonos származékúak, és kimutatható, hogy egy adott függvény antiderivatívája valójában egy olyan függvénycsalád, amely csak egy állandótól különbözik. Mivel az y = x2 + C függvény deriváltja, ahol C bármilyen állandó, y’ = 2x, az utóbbi antiderivatíváját a következők adják:

∫ 2 x D x = x 2 + C . {\displaystyle \ int 2x\,dx=x^{2}+C.}