raja-arvot ja infinitesimaalit
Calculus on yleensä kehitetty työstämällä hyvin pieniä määriä. Historiallisesti ensimmäinen tapa tehdä niin oli infinitesimaalit. Nämä ovat olioita, joita voidaan käsitellä reaalilukuina, mutta jotka ovat jossain mielessä ”äärettömän pieniä”. Esimerkiksi infinitesimaalinen luku voi olla suurempi kuin 0, mutta pienempi kuin mikään luku järjestyksessä 1, 1/2, 1/3, … ja siten vähemmän kuin mikään positiivinen reaaliluku. Tästä näkökulmasta calculus on kokoelma tekniikoita manipuloida infinitesimaaleja. Tunnukset D x {\displaystyle dx}
 ja D y {\displaystyle dy}
ja D y {\displaystyle dy}

pidettiin infinitesimaalisina, ja derivaatta d y/d x {\displaystyle dy / dx}

oli yksinkertaisesti niiden suhde.
infinitesimaalinen lähestymistapa putosi suosiosta 1800-luvulla, koska infinitesimaalin käsitettä oli vaikea tehdä täsmälliseksi. Käsite kuitenkin herätettiin henkiin 1900-luvulla ottamalla käyttöön epätyypillinen analyysi ja sileä infinitesimaalinen analyysi, joka tarjosi vankan perustan infinitesimaalien manipuloinnille.
1800-luvun lopulla infinitesimaalit korvattiin aatemaailmassa epsilonilla, Delta-lähestymistavalla rajoihin. Raja-arvot kuvaavat funktion arvoa tietyllä syötteellä sen arvojen mukaan lähellä olevilla syötteillä. Ne kuvaavat pienimuotoista käyttäytymistä reaalilukujärjestelmän yhteydessä. Tässä käsittelyssä, calculus on kokoelma tekniikoita manipuloida tiettyjä rajoja. Infinitesimaalit korvataan hyvin pienillä luvuilla, ja funktion äärettömän pieni käyttäytyminen löydetään ottamalla rajoittava käyttäytyminen pienemmille ja pienemmille luvuille. Rajat ajateltiin tarjota tiukempi perusta calculus, ja tästä syystä ne tuli standardi lähestymistapa aikana kahdennenkymmenennen vuosisadan.
Differentiaalilaskenta

Differentiaalilaskenta on funktion derivaatan määritelmän, ominaisuuksien ja sovellusten tutkimista. Derivaatan löytöprosessia kutsutaan differentioinniksi. Koska funktio ja piste alueella, derivaatta kyseisessä pisteessä on tapa koodata funktion pienimuotoista käyttäytymistä lähellä kyseistä pistettä. Löytämällä funktion derivaatta sen toimialueen jokaisesta pisteestä on mahdollista tuottaa Uusi funktio, jota kutsutaan derivaattafunktioksi tai pelkästään alkuperäisen funktion derivaataksi. Muodollisesti derivaatta on lineaarinen operaattori, joka ottaa funktion tulokseen ja tuottaa toisen funktion tulokseen. Tämä on abstraktimpaa kuin monet alkeis-algebrassa tutkitut prosessit, joissa funktiot yleensä syöttävät jonkin luvun ja tuottavat toisen luvun. Esimerkiksi jos tuplausfunktiolle annetaan tulo kolme, niin se tuottaa kuusi, ja jos neliöimisfunktiolle annetaan tulo kolme, niin se tuottaa yhdeksän. Derivaatta voi kuitenkin ottaa potenssifunktion tulona. Tämä tarkoittaa sitä, että derivaatta vie kaikki neliöintifunktion tiedot—kuten sen, että kaksi lähetetään neljälle, kolme lähetetään yhdeksälle, neljä lähetetään kuudelletoista ja niin edelleen—ja käyttää tätä tietoa toisen funktion tuottamiseen. Potenssifunktion synnyttämä funktio osoittautuu tuplausfunktioksi.
eksplisiittisemmin ”tuplausfunktiota” voidaan merkitä g(x) = 2x ja ”neliöfunktiota” F(x) = x2. ”Derivaatta ”ottaa nyt funktion f(x), joka määritellään lausekkeella” x2″, tulona, joka on kaikki tieto—kuten että kaksi lähetetään neljälle, kolme lähetetään yhdeksälle, neljä lähetetään kuudelletoista, ja niin edelleen—ja käyttää tätä tietoa tulostaakseen toisen funktion, funktio g(x) = 2x, kuten käy ilmi.
derivaatan yleisin symboli on heittomerkin kaltainen merkki, jota kutsutaan alkuluvuksi. Näin funktion F derivaatta merkitään f’: llä, joka lausutaan ”f alkuluku”. Esimerkiksi jos f (x) = x2 on neliöfunktio, niin f'(x) = 2x on sen derivaatta (tuplausfunktio g ylhäältä). Tämä notaatio tunnetaan Lagrangen notaationa.
Jos funktion tulo edustaa aikaa, derivaatta edustaa muutosta ajan suhteen. Esimerkiksi jos f on funktio, joka ottaa ajan tulona ja antaa pallon aseman sillä hetkellä ulostulona, niin F: n derivaatta on se, miten asema muuttuu ajassa, eli se on pallon nopeus.
Jos funktio on lineaarinen (eli jos funktion kuvaaja on suora), funktio voidaan kirjoittaa muodossa y = mx + b, jossa x on riippumaton muuttuja, y on riippuvainen muuttuja, b on y-leikkaus ja:
m = rise run = change in y change in x = Δ y Δ X . {\displaystyle m={\frac {\text{rise}}{\text{run}}}={\frac {{\text{change in}}} y} {{\text{change in}} x}}={\frac {\Delta y} {\Delta x}}.}

näin saadaan tarkka arvo suoran kaltevuudelle. Jos funktion kuvaaja ei kuitenkaan ole suora, niin Y: n muutos jaettuna X: n muutoksella vaihtelee. Johdannaiset antavat tarkan merkityksen tuotoksen muutoksen käsitteelle panoksen muutoksen suhteen. Olla konkreettinen, olkoon f on funktio, ja vahvistaa Kohta A alalla f. (A, f(A)) on piste kuvaajan funktio. Jos h on luku lähellä nollaa, niin A + h on luku lähellä a: ta.siksi (A + h, f(A + h)) on lähellä (a, f(a)). Näiden kahden pisteen välinen kaltevuus on
m = f ( A + h ) − f ( A ) ( A + h ) − A = f ( A + h ) − f ( A ) h . {\displaystyle m={\frac {f (A + h)-f(A)} {(A+h)-a}}={\frac {f(A+h) – f(A)} {h}}.}

tätä lauseketta kutsutaan differenssiosamääräksi. Käyrän kahden pisteen kautta kulkevaa suoraa kutsutaan sekanttijanaksi, joten m on sekanttijanan kulmakerroin välillä (A, f(a)) ja (A + h, f(A + h)). Sekanttiviiva on vain approksimaatio funktion käyttäytymiselle pisteessä A, koska se ei selitä, mitä tapahtuu a: n ja A: n + h: n välillä. ei ole mahdollista löytää käyttäytymistä A: ssa asettamalla h nollaksi, koska tämä vaatisi jakoa nollalla, mikä on määrittelemätön. Derivaatta määritellään ottamalla raja-arvo, kun h pyrkii nollaan, eli se pitää F: n käyttäytymistä kaikilla h: n pienillä arvoilla ja poimii johdonmukaisen arvon tapaukselle, jossa h on nolla:
lim H → 0 f ( A + h ) − f ( A ) h . {\displaystyle \lim _{h\To 0}{f (A + h) – f(a) \over {h}}.}

geometrisesti derivaatta on tangenttijanan kulmakerroin F: n kuvaajalle A: ssa. tangenttijana on sekanttijanojen raja siinä missä derivaatta on differenssiosamäärien raja. Tästä syystä derivaattaa kutsutaan joskus funktion F kulmakertoimeksi.
tässä on erityinen esimerkki, neliöfunktion derivaatta tulossa 3. Olkoon F(x) = x2 neliöfunktio.

f ′ ( 3 ) = lim h → 0 ( 3 + h ) 2 − 3 2 h = lim h → 0 9 + 6 h + h 2 − 9 h = lim h → 0 6 h + h 2 h = lim h → 0 ( 6 + h ) = 6 {\displaystyle {\begin{aligned}f'(3)&=\lim _{h\to 0}{(3+h)^{2}-3^{2} \over {h}}\\&=\lim _{h\to 0}{9+6h+h^{2}-9 \over {h}}\\&=\lim _{h\to 0}{6h+h^{2} \over {h}}\\&=\lim _{h\to 0}(6+h)\\&=6\end{aligned}}}

tangenttijanan kaltevuus neliöintifunktioon pisteessä (3, 9) on 6, eli se nousee kuusi kertaa nopeammin kuin se menee oikealle. Juuri kuvattu raja-arvoprosessi voidaan suorittaa mille tahansa neliöimisfunktion alueen pisteelle. Tämä määrittelee neliöfunktion derivaattafunktion tai vain neliöfunktion derivaatan lyhyeksi. Edellä esitetyn kaltainen laskenta osoittaa, että neliöfunktion derivaatta on tuplausfunktio.
Leibnizin notaatio
yleinen Leibnizin esittämä notaatio derivaatalle yllä olevassa esimerkissä on
y = x 2 D y D x = 2 x . {\displaystyle {\begin{aligned}y&=x^{2}\\{\frac {dy}{dx}}&=2x.\end{aligned}}}

raja-arvoihin perustuvassa lähestymistavassa symbolia dy/dx ei pidä tulkita kahden luvun osamääräksi vaan pikakirjoitukseksi yllä lasketulle rajalle. Leibniz kuitenkin halusi sen edustavan kahden äärettömän pienen luvun osamäärää, Dy on äärettömän pieni muutos y: ssä, joka johtuu äärettömän pienestä muutoksesta dx, jota sovelletaan X: ään. voimme myös ajatella, että D/dx on differentiaalioperaattori, joka ottaa funktion tulona ja antaa toisen funktion, derivaatan, ulostulona. Esimerkiksi:
d D x ( x 2 ) = 2 x . {\displaystyle {\frac {d}{DX}} (x^{2})=2x.}

tässä käytössä nimittäjän DX luetaan ”X: n suhteen”. Toinen esimerkki oikeasta merkintätavasta voisi olla:
G ( T ) = T 2 + 2 t + 4 D d D t g ( t ) = 2 t + 2 {\displaystyle {\begin{aligned}g(t)=T^{2}+2t+4\\\\{d \over DT}g(t)=2t+2\end{aligned}}}

silloinkin, kun Calculus on kehitetty käyttäen rajoja infinitesimaalien sijaan, on tavallista manipuloida symboleja kuten DX ja dy ikään kuin ne olisivat reaalilukuja; vaikka on mahdollista välttää tällaiset manipuloinnit, ne ovat joskus ei-loogisesti käteviä ilmaisemaan operaatioita, kuten kokonaisderivaatta.
Integraalilaskenta
Integraalilaskenta on kahden toisiinsa liittyvän käsitteen, epämääräisen integraalin ja definiittisen integraalin määritelmien, ominaisuuksien ja sovellusten tutkimus. Integraalin arvon löytämistä kutsutaan integraatioksi. Teknisessä kielenkäytössä integraalilaskenta tutkii kahta toisiinsa liittyvää lineaarista operaattoria.
epämääräinen integraali, joka tunnetaan myös nimellä antiderivatiivi, on derivaatan käänteisoperaatio. F on F: n epämääräinen integraali, kun f on F: n derivaatta. (Tämä ala-ja suuraakkosten käyttö funktiolle ja sen epämääräiselle integraalille on yleistä laskennassa.)
määräinen integraali syöttää funktion ja tuottaa luvun, joka antaa tulon kuvaajan ja x-akselin välisten alueiden algebrallisen summan. Määräisen integraalin teknisessä määrittelyssä on kyse suorakulmioiden pinta-alojen summan rajasta, jota kutsutaan Riemannin summaksi.
motivoiva esimerkki ovat tietyssä ajassa kuljetut etäisyydet.
D i S t a n c E = S p E E d ⋅ t i m e {\displaystyle \mathrm {Distance} =\mathrm {Speed} \cdot \mathrm {Time} }

Jos nopeus on vakio, tarvitaan vain kertolasku, mutta jos nopeus muuttuu, tarvitaan tehokkaampi tapa löytää etäisyys. Yksi tällainen menetelmä on likimääräinen kuljettu matka jakamalla ajan moniin lyhyisiin aikaväleihin, sitten kertomalla kunkin intervallin kulunut aika jollakin kyseisen intervallin nopeuksilla, ja sitten ottamalla summa (Riemannin summa) on likimääräinen kuljettu matka kussakin intervallissa. Perusajatus on, että jos vain vähän aikaa kuluu, niin vauhti pysyy kutakuinkin samana. Riemannin summa antaa kuitenkin vain likiarvon kuljetusta matkasta. Meidän on otettava raja kaikkien tällaisten Riemannin summia löytää tarkka matka matkusti.
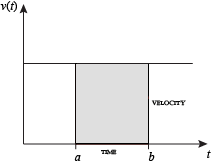

kun nopeus on vakio, kyseisellä ajanjaksolla kuljettu kokonaismatka voidaan laskea kertomalla nopeus ja aika. Esimerkiksi Matkustaminen tasaisesti 50 mph 3 tuntia johtaa yhteensä etäisyys 150 mailia. Kun vasemmalla olevassa kaaviossa kuvataan vakionopeutta ja aikaa, nämä kaksi arvoa muodostavat suorakulmion, jonka korkeus on yhtä suuri kuin nopeus ja leveys yhtä suuri kuin kulunut aika. Siksi nopeuden ja ajan tulo laskee myös suorakulmaisen alueen (vakio) nopeuskäyrän alle. Tämä yhteys kaaren alaisen alueen ja kuljetun matkan välillä voidaan ulottaa mihin tahansa epäsäännöllisen muotoiseen alueeseen, jolla esiintyy vaihtelevaa nopeutta tiettynä ajanjaksona. Jos oikealla olevassa kaaviossa f(x) kuvaa nopeutta, koska se vaihtelee ajan kuluessa, kuljettu matka (A: n ja b: n esittämien aikojen välillä) on varjostetun alueen s pinta-ala.
tämän alueen likimääräinen arvioimiseksi, intuitiivinen menetelmä olisi jakaa etäisyys A: n ja B: n välillä useampaan yhtä suureen segmenttiin, kunkin janan pituus, jota edustaa tunnus Δx. Jokaiselle pienelle segmentille voimme valita funktion f(x) yhden arvon. Kutsutaan, että arvo h. sitten alue suorakulmion pohja Δx ja korkeus h antaa matkan (aika Δx kerrottuna nopeudella h) matkusti kyseisessä segmentissä. Liittyy kunkin janan on keskimääräinen arvo funktion sen yläpuolella, f (x) = h. summa kaikkien tällaisten suorakulmioiden antaa likiarvo alueen välillä akselin ja käyrä, joka on likiarvo koko kuljetun matkan. Pienempi arvo Δx antaa enemmän suorakulmioita ja useimmissa tapauksissa parempi likiarvo, mutta tarkka vastaus meidän täytyy ottaa raja, koska Δx lähestyy nollaa.
integraation symboli on ∫ {\displaystyle \int}

, pitkänomainen S (S tarkoittaa ”summaa”). Definiittinen integraali kirjoitetaan seuraavasti: ∫ a b f (x) d x . {\displaystyle \int _{a}^{b}f (x)\, dx.}

ja luetaan ”integraali f-of-x: n A: sta b: hen X: n suhteen”. Leibnizin notaation DX tarkoituksena on ehdottaa käyrän alittavan alueen jakamista äärettömään määrään suorakulmioita, niin että niiden leveydestä Δx tulee äärettömän pieni DX. Raja-arvoihin perustuvan laskennan muotoilussa notaatio
∫ A B ⋯ D x {\displaystyle \int _{a}^{b}\cdots\, DX}

on ymmärrettävä operaattoriksi, joka ottaa funktion tulona ja antaa luvun, alueen, tulosteena. Päättyvä differentiaali, dx, ei ole luku, eikä sitä kerrota F(x): llä, vaikka Δx-rajamääritelmän muistutuksena sitä voidaan käsitellä sellaisenaan integraalin symbolisissa käsittelyissä. Muodollisesti differentiaali ilmaisee muuttujan, jonka yli funktio on integroitu, ja toimii integraatiooperaattorin sulkusulkuna.
epämääräinen integraali eli antiderivatiivi kirjoitetaan:
∫ f ( x ) D x . {\displaystyle \int f (x)\, dx.}

funktioilla, jotka eroavat vain vakiolla, on sama derivaatta, ja voidaan osoittaa, että tietyn funktion antiderivatiivi on todellisuudessa funktioiden perhe, joka eroaa vain vakiolla. Koska funktion y = x2 + C derivaatta, jossa C on mikä tahansa vakio, on y’ = 2x, jälkimmäisen antiderivatiivin antaa:
∫ 2 x D x = x 2 + C . {\displaystyle \int 2x\,dx=x^{2}+C.}

epämääräisessä integraalissa eli antiderivatiivissa esiintyvä määrittelemätön vakio C tunnetaan integraation vakiona.
peruslause
calculuksen peruslause toteaa, että differentiaatio ja integraatio ovat käänteisiä operaatioita. Tarkemmin se suhteuttaa antiderivatiivien arvot definiittisiin integraaleihin. Koska antiderivatiivin laskeminen on yleensä helpompaa kuin definiittisen integraalin määritelmän soveltaminen, calculuksen peruslause tarjoaa käytännöllisen tavan laskea definiittisiä integraaleja. Se voidaan myös tulkita täsmälliseksi toteamukseksi siitä, että eriyttäminen on integraation käänteispuoli.
calculuksen tilojen peruslause: Jos funktio f on intervallilla jatkuva ja jos F on funktio, jonka derivaatta on intervallilla f (A, b), niin
∫ a b f ( x ) D x = F ( b ) − F ( A ) . {\displaystyle \int _{a}^{b}f(x)\,dx=F(b)-F (A).}

lisäksi jokaista intervallin (a, b) x ∫ x f ( t ) d t = f ( x ) . {\displaystyle {\frac {d}{dx}}\int _{a}^{x}f(t)\,dt=f (x).}

tämä oivallus, jonka tekivät sekä Newton että Leibniz, jotka perustivat tuloksensa Isaac Barrow ’ n aikaisempaan työhön, oli avain analyyttisten tulosten leviämiseen sen jälkeen, kun heidän työnsä tuli tunnetuksi. Peruslause tarjoaa algebrallisen menetelmän laskea monia definiittisiä integraaleja – suorittamatta raja-prosesseja-etsimällä kaavoja antiderivatiiveille. Se on myös differentiaaliyhtälön prototyyppiratkaisu. Differentiaaliyhtälöt liittävät tuntemattoman funktion sen johdannaisiin, ja ovat kaikkialla tieteissä.