Calculus

differentiel beregning er undersøgelsen af definitionen, egenskaberne og anvendelserne af derivatet af en funktion. Processen med at finde derivatet kaldes differentiering. Givet en funktion og et punkt i domænet er derivatet på det tidspunkt en måde at kode for funktionens lille opførsel nær dette punkt. Ved at finde derivatet af en funktion på hvert punkt i sit domæne er det muligt at producere en ny funktion, kaldet derivatfunktionen eller bare derivatet af den oprindelige funktion. Formelt set er derivatet en lineær operatør, der tager en funktion som input og producerer en anden funktion som output. Dette er mere abstrakt end mange af de processer, der studeres i elementær algebra, hvor funktioner normalt indtaster et tal og udsender et andet tal. For eksempel, hvis fordoblingsfunktionen får input tre, udsender den seks, og hvis kvadratfunktionen får input tre, udsender den ni. Derivatet kan dog tage kvadratfunktionen som input. Dette betyder, at derivatet tager al information om kvadratfunktionen—såsom at to sendes til fire, tre sendes til ni, fire sendes til seksten osv.—og bruger disse oplysninger til at producere en anden funktion. Funktionen produceret ved at udlede kvadratfunktionen viser sig at være fordoblingsfunktionen.

i mere eksplicitte termer kan “fordoblingsfunktionen” betegnes med g(H) = 2 gange og “kvadratfunktionen” med f(H) = H2. “Derivatet” tager nu funktionen f (h), defineret af udtrykket” H2″, som et input, det vil sige al information—som at to sendes til fire, tre sendes til ni, fire sendes til seksten osv.—og bruger disse oplysninger til at udsende en anden funktion, Funktionen g(H) = 2 gange, som det vil vise sig.

det mest almindelige symbol for et derivat er et apostroflignende mærke kaldet prime. Således er derivatet af en funktion kaldet f betegnet med f’, udtalt”f prime”. For eksempel, hvis f(h) = H2 er kvadratfunktionen, så er f'(H) = 2 gange dens derivat (fordoblingsfunktionen g ovenfra). Denne notation er kendt som Lagrange ‘ s notation.

Hvis input af funktionen repræsenterer tid, repræsenterer derivatet ændring med hensyn til tid. For eksempel, hvis f er en funktion, der tager en tid som input og giver positionen af en bold på det tidspunkt som output, så er derivatet af f, hvordan positionen ændrer sig i tide, det vil sige, det er kuglens hastighed.

Hvis en funktion er lineær (dvs .hvis grafen for funktionen er en lige linje), kan funktionen skrives som y = MH + b, hvor H er den uafhængige variabel, y er den afhængige variabel, b er y-skæringspunktet, og:

m = rise run = change in y change in H = Change y. {\displaystyle m={\frac {\tekst{rise}} {\tekst{run}}}={\frac {{\tekst{change in }}y} {{\tekst{change in}}}} = {\frac {\Delta y} {\Delta y}}.}

dette giver en nøjagtig værdi for hældningen af en lige linje. Hvis grafen for funktionen ikke er en lige linje, varierer ændringen i y divideret med ændringen i h. Derivater giver en nøjagtig betydning for begrebet ændring i output med hensyn til ændring i input. For at være konkret, lad f være en funktion, og fastgør et punkt A i domænet for f. (A, f(A)) er et punkt på grafen for funktionen. Hvis h er et tal tæt på nul, er a + h et tal tæt på a. derfor er (A + h, f(A + h)) tæt på (A, f(A)). Hældningen mellem disse to punkter er

m = f ( A + h ) − f ( A ) ( A + h ) − A = f ( A + h ) − F ( A ) h . {\displaystyle m={\frac {f (A + h)-f(A)} {(A+h)-A}}={\frac {f(A+h) – f(A)} {h}}.}

dette udtryk kaldes en forskelskvotient. En linje gennem to punkter på en kurve kaldes en sekantlinie, så m er hældningen af sekantlinjen mellem (A, f(A)) og (A + h, f(A + h)). Secant-linjen er kun en tilnærmelse til funktionens opførsel ved punkt A, fordi den ikke tager højde for, hvad der sker mellem A og A + h. det er ikke muligt at opdage adfærden ved A ved at indstille h til nul, fordi dette ville kræve opdeling med nul, hvilket er udefineret. Derivatet defineres ved at tage grænsen, da h har tendens til at være nul, hvilket betyder, at det betragter opførslen af f for alle små værdier af h og udtrækker en konsistent værdi for sagen, når h er lig med nul:

lim h − kur 0 F ( A + h) – F ( A ) h . {\displaystyle \ lim _{h \ til 0}{f(A+h)-f(A) \over {h}}.}

Geometrisk er derivatet hældningen af tangentlinjen til grafen for f ved a. tangentlinjen er en grænse for sekantlinjer, ligesom derivatet er en grænse for forskelskvotienter. Af denne grund kaldes derivatet undertiden hældningen af funktionen f.

Her er et bestemt eksempel, derivatet af kvadratfunktionen ved indgangen 3. Lad f (H) = H2 være kvadratfunktionen.

derivatet f'(H) af en kurve på et punkt er hældningen af linjen tangent til den kurve på det tidspunkt. Denne hældning bestemmes ved at overveje grænseværdien af skråningerne af sekantlinjer. Tangentlinjen (i grøn), der passerer gennem punktet (-3/2, -15/8) har en hældning på 23/4. Bemærk, at de lodrette og vandrette skalaer i dette billede er forskellige.

f ′ ( 3 ) = lim h → 0 ( 3 + h ) 2 − 3 2 h = lim h → 0 9 + 6 h + h 2 − 9 h = lim h → 0 6 h + h 2 h = lim h → 0 ( 6 + h ) = 6 {\displaystyle {\begin{aligned}f'(3)&=\lim _{h\to 0}{(3+h)^{2}-3^{2} \over {h}}\\&=\lim _{h\to 0}{9+6h+h^{2}-9 \over {h}}\\&=\lim _{h\to 0}{6h+h^{2} \over {h}}\\&=\lim _{h\to 0}(6+h)\\&=6\end{aligned}}}

hældningen af tangentlinjen til kvadratfunktionen ved punktet (3, 9) er 6, det vil sige, det går op seks gange så hurtigt som det går til højre. Den netop beskrevne grænseproces kan udføres for ethvert punkt i domænet for kvadratfunktionen. Dette definerer den afledte funktion af kvadratfunktionen eller bare derivatet af kvadratfunktionen for kort. En beregning svarende til ovenstående viser, at derivatet af kvadratfunktionen er fordoblingsfunktionen.

leibnis notation

en fælles notation, introduceret af Leibnis, for derivatet i eksemplet ovenfor er

y = 2 d y d = 2 gange . {\displaystyle {\begin{aligned}y&=H^{2}\\{\frac {dy}{DH}}&=2h.\end{aligned}}}

i en tilgang baseret på grænser skal symbolet dy / DKs fortolkes ikke som kvotienten for to tal, men som en stenografi for grænsen beregnet ovenfor. Vi kan også tænke på d / D som en differentieringsoperatør, der tager en funktion som input og giver en anden funktion, derivatet, som output. For eksempel:

d d ( 2 ) = 2 gange . {\displaystyle {\frac {d} {d}} (h^{2})=2h.}

i denne brug læses DC i nævneren som “med hensyn til H”. Et andet eksempel på korrekt notation kunne være:

g ( t ) = t 2 + 2 t + 4 D d T g ( t ) = 2 T + 2 {\displaystyle {\begin{aligned}g(t)=t^{2}+2T+4\\\\{d \over dt}g(t)=2T+2\end{aligned}}}

selv når beregning er udviklet ved hjælp af grænser snarere end uendelige, er det almindeligt at manipulere symboler som f.eks.

Integral calculus

Integral calculus er studiet af definitioner, egenskaber og anvendelser af to relaterede begreber, det ubestemte integral og det bestemte integral. Processen med at finde værdien af en integral kaldes integration. På teknisk sprog studerer integral calculus to relaterede lineære operatører.

den ubestemte integral, også kendt som antiderivativ, er den inverse operation til derivatet. F er et ubestemt integral af f, når f er et derivat af F. (Denne brug af små og store bogstaver for en funktion og dens ubestemte integral er almindelig i calculus.)

de bestemte integrerede indgange en funktion og udsender et tal, hvilket giver den algebraiske sum af områder mellem grafen for input og H-aksen. Den tekniske definition af det bestemte integral involverer grænsen for en sum af områder med rektangler, kaldet A Riemann sum.

et motiverende eksempel er de tilbagelagte afstande på et givet tidspunkt.

D i S T a n C E = S P e e D list t I m e {\displaystyle \mathrm {Distance} =\mathrm {Speed} \cdot \mathrm {Time} }

Hvis hastigheden er konstant, er kun multiplikation nødvendig, men hvis hastigheden ændres, er en mere kraftfuld metode til at finde afstanden nødvendig. En sådan metode er at tilnærme den tilbagelagte afstand ved at opdele tiden i mange korte tidsintervaller og derefter multiplicere den forløbne tid i hvert interval med en af hastighederne i dette interval og derefter tage summen (en Riemann-sum) af den omtrentlige tilbagelagte afstand i hvert interval. Grundtanken er, at hvis der kun går kort tid, forbliver hastigheden mere eller mindre den samme. En Riemann-sum giver dog kun en tilnærmelse af den tilbagelagte afstand. Vi må tage grænsen for alle sådanne Riemann-summer for at finde den nøjagtige tilbagelagte afstand.

integration kan betragtes som måling af området under en kurve, defineret af F(H), mellem to punkter (her a og B).

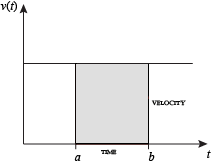
når hastigheden er konstant, kan den samlede tilbagelagte afstand over det givne tidsinterval beregnes ved at multiplicere hastighed og tid. For eksempel, rejser en stabil 50 mph for 3 timer resulterer i en samlet afstand på 150 miles. I diagrammet til venstre, når konstant hastighed og tid tegnes, danner disse to værdier et rektangel med højde svarende til hastigheden og bredden svarende til den forløbne tid. Derfor beregner produktet af hastighed og tid også det rektangulære område under (konstant) hastighedskurven. Denne forbindelse mellem området under en kurve og tilbagelagt afstand kan udvides til ethvert uregelmæssigt formet område, der udviser en svingende hastighed over en given tidsperiode. Hvis F (H) i diagrammet til højre repræsenterer hastighed, da den varierer over tid, er den tilbagelagte afstand (mellem tiderne repræsenteret af A og b) området for det skraverede område s.

for at tilnærme dette område ville en intuitiv metode være at opdele afstanden mellem A og b i et antal lige store segmenter, længden af hvert segment repræsenteret af symbolet. For hvert lille segment kan vi vælge en værdi af funktionen f (h). Ring til denne værdi h. derefter giver området af rektanglet med basishøjde og højde h afstanden (Tidshøjde ganget med hastighed h), der er tilbagelagt i dette segment. Summen af alle sådanne rektangler giver en tilnærmelse af området mellem aksen og kurven, hvilket er en tilnærmelse af den samlede tilbagelagte afstand. En mindre værdi vil give flere rektangler og i de fleste tilfælde en bedre tilnærmelse, men for et præcist svar er vi nødt til at tage en grænse, da den nærmer sig nul.

integrationssymbolet er {\displaystyle \int}

, en langstrakt S (S står for “sum”). Det bestemte integral er skrevet som: – A B f (H ) D H . {\displaystyle \ int _{a}^{b}f (S)\, DS.}

og læses “integralet fra a til b af f-of-H med hensyn til”. I en formulering af beregningen baseret på grænser skal notationen

list a b list d {\displaystyle \int _{a}^{b}\cdots\, d}

forstås som en operatør, der tager en funktion som input og giver et tal, området, som et output. Den endelige differentiering er ikke et tal og multipliceres ikke med f, selvom den tjener som en påmindelse om definitionen af grænseværdien, kan den behandles som sådan i symbolske manipulationer af integralet. Formelt angiver differencen den variabel, over hvilken funktionen er integreret, og fungerer som en lukkebeslag for integrationsoperatøren.

den ubestemte integral, eller antiderivativ, er skrevet:

{\displaystyle \ int f (s)\,DS.}

funktioner, der kun adskiller sig med en konstant, har det samme derivat, og det kan vises, at antiderivativet for en given funktion faktisk er en familie af funktioner, der kun adskiller sig med en konstant. Da derivatet af funktionen y = 2 + C, hvor C er en hvilken som helst konstant, er y’ = 2 gange, er antiderivativet af sidstnævnte givet ved:

2 gange 2 + c . {\displaystyle \ int 2H\, DH=^{2} + C.}

den uspecificerede konstant C til stede i den ubestemte integral eller antiderivativ er kendt som integrationskonstanten.

grundlæggende sætning

Hovedartikel: grundlæggende sætning i calculus

den grundlæggende sætning i calculus siger, at differentiering og integration er inverse operationer. Mere præcist relaterer det værdierne af antiderivativer til bestemte integraler. Fordi det normalt er lettere at beregne en antiderivativ end at anvende definitionen af en bestemt integral, giver den grundlæggende sætning i calculus en praktisk måde at beregne bestemte integraler på. Det kan også fortolkes som en præcis erklæring om, at differentiering er det omvendte af integration.

den grundlæggende sætning af calculus stater: Hvis en funktion f er kontinuerlig på intervallet, og hvis F er en funktion, hvis derivat er f på intervallet (a, b), så

{\displaystyle \ int _{a}^{b}f (H)\, D=F(b)-F (A).}

desuden for hver h i intervallet (a, b),

d d h h f ( t ) d t = f ( H ) . {\displaystyle {\frac {d}} \ int _{a}^{H} f(t)\,dt=f (H).}

denne erkendelse, foretaget af både Nyton og Leibnis, der baserede deres resultater på tidligere arbejde af Isaac barv, var nøglen til spredning af analytiske resultater, efter at deres arbejde blev kendt. Den grundlæggende sætning giver en algebraisk metode til beregning af mange Bestemte integraler—uden at udføre grænseprocesser—ved at finde formler til antiderivativer. Det er også en prototype løsning af en differentialligning. Differentialligninger relaterer en ukendt funktion til dens derivater og er allestedsnærværende inden for videnskaberne.