Limity a drobnosti
počet je obvykle vyvinuté tím, že pracuje s velmi malým množství. Historicky první způsob, jak toho dosáhnout, byl infinitezimály. Jedná se o objekty, s nimiž lze zacházet jako s reálnými čísly, ale které jsou v jistém smyslu „nekonečně malé“. Například infinitezimální číslo může být větší než 0, ale menší než libovolné číslo v pořadí 1, 1/2, 1/3, … a tedy méně než jakékoliv kladné reálné číslo. Z tohoto pohledu je počet sbírkou technik pro manipulaci s nekonečnými čísly. Symboly d x {\displaystyle dx}

a d y {\displaystyle dy}

byly pořízeny být nekonečně malé, a derivace d y / d x {\displaystyle dy/dx}

byla prostě jejich poměr.
infinitezimální přístup vypadl z laskavosti v 19. století, protože to bylo obtížné, aby se pojem nekonečně přesné. Nicméně, koncept byl oživen ve 20. století se zavedením non-standardní analýzy a hladké infinitezimální analýzy, která poskytla pevné základy pro manipulaci drobnosti.
na konci 19. století byly infinitesimály nahrazeny v akademické sféře Epsilon, delta přístupem k limitům. Limity popisují hodnotu funkce na určitém vstupu z hlediska jejích hodnot na blízkých vstupech. Zachycují chování malého rozsahu v kontextu systému reálných čísel. Při této léčbě je počet souborem technik pro manipulaci s určitými limity. Infinitesimals se nahradí velmi malými čísly a nekonečně malé chování funkce se zjistí tím, že se omezí chování pro menší a menší čísla. Předpokládalo se, že limity poskytují přísnější základ pro počet, a proto se během dvacátého století staly standardním přístupem.
Diferenciální počet

Diferenciální počet je studium definice, vlastností a aplikací derivátu funkce. Proces nalezení derivátu se nazývá diferenciace. Vzhledem k funkci a bodu v doméně je derivace v tomto bodě způsobem kódování chování funkce v malém měřítku poblíž tohoto bodu. O nalezení derivace funkce v každém bodě v jeho domény, je možné vytvořit nové funkce, nazývá derivace funkce, nebo jen derivace původní funkce. Formálně, derivace je lineární operátor, který bere funkci jako svůj vstup a produkuje druhou funkci jako svůj výstup. To je abstraktnější než mnoho procesů studovaných v elementární algebře, kde funkce obvykle zadávají číslo a vydávají jiné číslo. Například, pokud je funkce zdvojnásobení dána vstupem tři, pak vypíše šest a pokud je funkce kvadratury dána vstupem tři, pak vyvede devět. Derivace však může mít funkci kvadratury jako vstup. To znamená, že derivát bere všechny informace o funkci kvadratury—například že dvě jsou odeslány na čtyři, tři jsou odeslány na devět, čtyři jsou odeslány na šestnáct atd. – a používá tyto informace k vytvoření jiné funkce. Funkce vytvořená odvozením funkce kvadratury se ukáže jako funkce zdvojnásobení.
v jasnějších termínech může být „funkce zdvojnásobení“ označena g (x) = 2x a „funkce kvadratury“ F (x) = x2. „Derivát“ nyní zastává funkci f(x), definovaný výraz „x2“, jako vstup, který je všechny informace—například, že dva je poslal na čtyři, tři je poslal na devět, čtyři je poslal na šestnáct, a tak dále—a používá tyto informace k výkonu jiné funkce, funkce g(x) = 2x, jak dopadne.
nejběžnějším symbolem derivace je značka podobná apostrofu zvaná prime. Derivace funkce nazvané f je tedy označena F‘, vyslovuje se „F prime“. Například, pokud f (x) = x2 je funkce kvadratury, pak f'(x) = 2x je její derivace (funkce zdvojnásobení g shora). Tato notace je známá jako Lagrangeova notace.
Pokud vstup funkce představuje čas, pak derivace představuje změnu vzhledem k času. Například, pokud f je funkce, která bere čas jako vstup a dává pozici míč v té době jako výstup, pak derivace f je jak poloha se mění v čase, to je, to je rychlost míče.pokud je graf funkce přímka), pak může být funkce zapsána jako y = mx + b, kde x je nezávislá proměnná, y je závislá proměnná, b je y-intercept a:
m = rise run = změna v y změna v x = Δ y Δ x . {\displaystyle m={\frac {\text{růst}}{\text{run}}}={\frac {{\text{změna v }}y}{{\text{změna v }}x}}={\frac {\Delta y}{\Delta x}}.}

to dává přesnou hodnotu pro sklon přímky. Pokud graf funkce není přímka, pak se změna y dělená změnou x liší. Deriváty dávají přesný význam pojmu změny výstupu s ohledem na změnu vstupu. Být konkrétní, nechť f je funkce, a opravit bodu a v oblasti f. (a, f(a)) je bod na grafu funkce. Pokud je h číslo blízké nule, pak a + h je číslo blízké a. proto(A + h, f (A + h)) je blízko (a, f(a)). Sklon mezi těmito dvěma body je
m = f (A + h) – f (a) (a + h) – A = f (A + h ) – f (A) h . {\displaystyle m={\frac {f (A + h) – f (A)} {(a + h) – a}} = {\frac {f (A+h) – f (A)} {h}}.}

tento výraz se nazývá rozdílový kvocient. Linka přes dva body na křivce se nazývá sečna, takže “ m “ je směrnice sečny mezi (a, f(a)) a (a + h, f(a + h)). Sečny je jen aproximaci chování funkce v bodě a, protože to nebere v úvahu, co se děje mezi a a a + h. To není možné zjistit chování na nastavení h na nulu, protože to by vyžadovalo dělení nulou, což je nedefinované. Derivace je definována tím, že limita h k nule, což znamená, že se domnívá, že chování f pro všechny malé hodnoty h a výtažky konzistentní hodnota pro případ, když se h rovná nule,
lim h → 0 f ( a + h ) − f ( a ) h . {\displaystyle \ lim _{h \ to 0}{f (A+h) – f (A) \over {h}}.}

Geometricky derivace je směrnice tečny ke grafu f v a. Tečna je limit sečny řádky jen jako derivace je limit, rozdíl, podíl, kde v čitateli. Z tohoto důvodu se derivace někdy nazývá sklon funkce f.
zde je konkrétní příklad, derivace funkce kvadratury na vstupu 3. Nechť f (x) = x2 je funkce kvadratury.

f ′ ( 3 ) = lim h → 0 ( 3 + h ) 2 − 3 2 h = lim h → 0 9 + 6 h + h 2 − 9 h = lim h → 0 6 h + h 2 h = lim h → 0 ( 6 + h ) = 6 {\displaystyle {\begin{aligned}f'(3)&=\lim _{h\to 0}{(3+h)^{2}-3^{2} \over {h}}\\&=\lim _{h\to 0}{9+6h+h^{2}-9 \over {h}}\\&=\lim _{h\to 0}{6h+h^{2} \over {h}}\\&=\lim _{h\to 0}(6+h)\\&=6\end{aligned}}}

směrnici tečny k kvadratura funkce v bodě (3, 9) je 6, to znamená, že to bude až šest krát tak rychle, jak to bude správné. Právě popsaný limitní proces lze provést pro libovolný bod v doméně kvadratické funkce. To definuje derivační funkci kvadratické funkce nebo zkrátka derivaci kvadratické funkce. Výpočet podobný výše uvedenému ukazuje, že derivace funkce kvadratury je funkce zdvojnásobení.
Leibnitzovu notaci
běžná notace, zavedl Leibniz, pro derivace ve výše uvedeném příkladu je
y = x 2 d y d x = 2 x . {\displaystyle {\begin{aligned}y&=x^{2}\\{\frac {dy}{dx}}&=2x.\end{aligned}}}

v přístupu založeném na limitech nesmí být symbol dy / dx interpretován jako kvocient dvou čísel, ale jako zkratka pro limit vypočítaný výše. Leibniz však zamýšlel reprezentovat podílem dvou nekonečně malých čísel, dy jsou nekonečně malé změny v y způsobené nekonečně malou změnou dx aplikován na x. Můžeme také si myslím, že d/dx jako diferenciace operátor, který má funkce jako vstupní a dává další funkce, derivace, jako výstupní. Například:
d d x (x 2) = 2 x . {\displaystyle {\frac {d}{dx}}(x^{2})=2x.}

V tomto použití, dx ve jmenovateli je číst jako „s ohledem na x“. Dalším příkladem správného zápisu může být:
g ( t ) = t 2 + 2 t + 4 d d t g ( t ) = 2 t + 2 {\displaystyle {\begin{aligned}g(t)=t^{2}+2t+4\\\\{d \nad dt}g(t)=2t+2\end{aligned}}}

I když kalkul je vytvořena pomocí limity spíše než drobnosti, je běžné, manipulovat symboly jako dx a dy, jako kdyby byly reálných čísel; i když je možné, aby se zabránilo takové manipulace, někdy jsou notationally výhodné v tom, vyjadřující operace jako totální derivace.
Integrální počet
Integrální počet je studium definice, vlastnosti, a použití dvou souvisejících pojmů, neurčitý integrál a určitý integrál. Proces hledání hodnoty integrálu se nazývá integrace. V technickém jazyce studuje integrální počet dva příbuzné lineární operátory.
neurčitý integrál, známý také jako antiderivativ, je inverzní operace k derivaci. F je neurčitý integrál f, když f je derivace F. (Toto použití malých a velkých písmen pro funkci a její neurčitý integrál je běžné v počtu.)
definitivní integrální vstupy funkci a výstupy číslo, které dává algebraický součet oblastí mezi grafem vstupu a osou x. Technická definice určitého integrálu zahrnuje limit součtu ploch obdélníků, nazývaných Riemannův součet.
motivujícím příkladem jsou ujeté vzdálenosti v daném čase.
D i s t a n c e = S p e e d ⋅ T i m e {\displaystyle \mathrm {Vzdálenost} =\mathrm {Rychlost} \cdot \mathrm {Čas} }

v Případě, že rychlost je konstantní, pouze násobení je potřeba, ale pokud se rychlost mění, výkonnější způsob zjištění vzdálenosti je nutné. Jedna taková metoda je přibližná vzdálenost, kterou rozbití do mnoha krátkých časových intervalech, pak vynásobením čas, který uplynul v každém intervalu o jednu z rychlostí v intervalu, a pak brát součet (Riemann sum) přibližná ujetá vzdálenost v každém intervalu. Základní myšlenkou je, že pokud uplyne jen krátká doba, rychlost zůstane víceméně stejná. Riemannova suma však dává pouze přibližnou vzdálenost. Musíme vzít limit všech takových Riemannových částek, abychom našli přesnou ujetou vzdálenost.
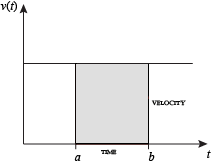

je-li rychlost konstantní, lze celkovou vzdálenost ujetou v daném časovém intervalu vypočítat vynásobením rychlosti a času. Například cestování stabilní 50 mph po dobu 3 hodin vede k celkové vzdálenosti 150 mil. V diagramu vlevo, když jsou grafovány konstantní rychlost a čas, Tvoří tyto dvě hodnoty obdélník s výškou rovnou rychlosti a šířce rovnající se uplynulému času. Proto součin rychlosti a času také vypočítá obdélníkovou plochu pod křivkou (konstantní) rychlosti. Toto spojení mezi oblastí pod křivkou a ujetou vzdáleností může být rozšířeno na jakoukoli nepravidelně tvarovanou oblast vykazující kolísající rychlost v daném časovém období. Je-li f(x) v diagramu na pravé straně představuje rychlost, jak se to mění v průběhu času, ujeté vzdálenosti (mezi časy zastoupeny a, b) je plocha té vystínované oblasti.
Pro přibližné oblasti, intuitivní metoda by se rozdělit vzdálenost mezi a a b do mnoha rovných segmentů, délka každého segmentu reprezentován symbolem Δx. Pro každý malý segment můžeme zvolit jednu hodnotu funkce f (x). Říkat, že hodnota h. Pak plocha obdélníku se základnou Δx a výšce h udává vzdálenost (čas Δx násobí rychlost h) cestoval v tomto segmentu. Spojené s každý segment je průměrná hodnota funkce výše, f(x) = h. Součet všech těchto obdélníků dává aproximaci plochy mezi osou a křivkou, která je aproximace celkové ujeté vzdálenosti. Menší hodnota pro Δx poskytne více obdélníků a ve většině případů lepší aproximaci, ale pro přesnou odpověď musíme vzít limit, protože Δx se blíží nule.
symbol integrace, je ∫ {\displaystyle \int }

, protáhlý S (S je zkratka pro „částka“). Určitý integrál je zapsán jako: .a b f (x ) d x. {\displaystyle \int _{a}^{b}f (x)\, dx.}

a je četl „integrál od a do b z f-o-x vzhledem k x.“ Leibnitzovu notaci dx je určena navrhnout dělící plochu pod křivkou na nekonečný počet obdélníků, tak, že jejich šířka Δx stává nekonečně malé dx. Ve složení je z kalkulu na základě limitů, zápis,
∫ a b ⋯ d x {\displaystyle \int _{a}^{b}\cdots \,dx}

je třeba chápat jako subjekt, který má fungovat jako vstupní a dává číslo, oblast, jako výstupní. Koncový diferenciál, dx, není číslo a není vynásoben f (x), i když slouží jako připomínka definice limitu Δx, lze s ním zacházet jako s symbolickými manipulacemi integrálu. Formálně diferenciál označuje proměnnou, nad kterou je funkce integrována, a slouží jako uzavírací konzola pro integrační operátor.
neurčitý integrál nebo antiderivativ je zapsán:
f f (x) d x . {\displaystyle \int f(x)\,dx.}

Funkce se liší pouze o konstanty mají stejnou derivaci, a to může být ukázáno, že integrál z dané funkce je vlastně rodina funkcí, liší se pouze konstantní. Protože derivace funkce y = x2 + C, kde C je libovolná konstanta, je y‘ = 2x, primitivní funkce ta je dána tím, že:
∫ 2 x d x = x 2 + C . {\displaystyle \int 2x\,dx=x^{2}+C}

nespecifikovaná konstanta C přítomen v neurčitý integrál nebo primitivní funkce je známá jako konstanta integrace.
Základní věta
základní věta kalkulu uvádí, že diferenciace a integrace jsou inverzní operace. Přesněji řečeno, spojuje hodnoty antiderivativ s určitými integrály. Protože je obvykle jednodušší vypočítat primitivní funkce, než použít definici integrálu, základní věta kalkulu, poskytuje praktický způsob výpočtu určitých integrálů. Lze jej také interpretovat jako přesné prohlášení o tom, že diferenciace je inverzní integrací.
Základní věta stavů počtu: Pokud je funkce f spojitá v intervalu a pokud F je funkce, jejíž derivace je f v intervalu (a, b), pak
∫ A b f (x) d x = F ( b ) − F ( a ) . {\displaystyle\int _{a}^{b}f(x)\, dx=F(b)-F(A).}

dále pro každé x v intervalu ( a, b),
d d x ∫ a x f ( t ) d T = f (x ) . {\displaystyle {\frac {d}{dx}}\int _{a}^{x}f(t)\,dt=f (x).}

tato realizace, kterou provedli Newton i Leibniz, kteří založili své výsledky na dřívější práci Isaaca Barrowa, byla klíčem k šíření analytických výsledků poté, co se jejich práce stala známou. Základní věta nabízí algebraické metody výpočetní mnoho integrálů—bez provedení omezit procesy—najít vzorce pro primitivní funkce. Je to také prototyp řešení diferenciální rovnice. Diferenciální rovnice vztahují neznámou funkci k jejím derivátům a jsou všudypřítomné ve vědách.